How to Approximate the Sine Function Using the Taylor or Maclaurin Polynomial
In this exercise, we aim to approximate the sine function using a Taylor polynomial.
$$ f(x) = \sum_{k=0}^{n} \frac{f^{(k)}(x_0)}{k!} \cdot (x - x_0)^k + R_n(x) $$
We select the center at x0 = 0 so as to simplify the calculation to the Maclaurin series, and choose the polynomial degree n = 5.
Note. The Maclaurin series is essentially the Taylor polynomial centered at x0 = 0. Calculations are often considerably simpler in this form. Thus, whenever possible, it’s advantageous to choose x0 = 0 and work within the Maclaurin framework.
To construct the polynomial, we calculate each term of the Taylor series separately, from the first term (n = 0) up to the fifth (n = 5).
We then add Peano’s remainder term at the end.
Degree n = 0
$$ \frac{D^{0} \sin 0 }{0!} \cdot (x - 0)^0 $$
$$ \frac{\sin 0}{1} \cdot 1 $$
$$ = 0 $$
The first term of the series is zero.
Degree n = 1
$$ \frac{D^{1} \sin 0 }{1!} \cdot (x - 0)^1 $$
$$ \frac{\cos 0}{1} \cdot x $$
$$ = x $$
The second term of the series is x.
Degree n = 2
$$ \frac{D^{2} \sin 0 }{2!} \cdot (x - 0)^2 $$
$$ \frac{-\sin 0}{2!} \cdot x^2 $$
$$ = 0 $$
The third term of the series is zero.
Degree n = 3
$$ \frac{D^{3} \sin 0 }{3!} \cdot (x - 0)^3 $$
$$ \frac{-\cos 0}{3!} \cdot x^3 $$
$$ = \frac{-1}{3!} \, x^3 $$
The fourth term of the series is -x3/3!.
Note. Instead of recalculating higher-order derivatives of the sine function from scratch at every step, it’s more efficient to simply differentiate the previous derivative. For instance, for n = 2, the derivative is -sin(0). Differentiating this yields D(-sin(0)) = -cos(0), providing the third derivative directly.
Degree n = 4
$$ \frac{D^{4} \sin 0 }{4!} \cdot (x - 0)^4 $$
$$ \frac{\sin 0}{4!} \cdot x^4 $$
$$ = 0 $$
The fifth term of the series is zero.
Degree n = 5
$$ \frac{D^{5} \sin 0 }{5!} \cdot (x - 0)^5 $$
$$ \frac{\cos 0}{5!} \cdot x^5 $$
$$ = \frac{1}{5!} \, x^5 $$
The sixth term of the series is x5/5!.
We have now determined all the terms of the Taylor polynomial up to degree n = 5.
All that remains is to compute the remainder term.
Peano’s Remainder
Peano’s remainder is expressed using little-o notation:
$$ R_n = o((x - x_0)^n) $$
Given that x0 = 0 and n = 5:
$$ R_5 = o((x - 0)^5) $$
$$ R_5 = o(x^5) $$
Note. The little-o notation indicates that the remainder Rn is of higher order than x5. In other words, it approaches zero faster than x5 as x approaches x0. $$ \lim_{x \rightarrow x_0} \frac{R_n}{(x - x_0)^n} = 0 $$
We can now write the complete Taylor polynomial by summing all the computed terms:
$$ p_5 = 0 + x + 0 - \frac{x^3}{3!} + 0 + \frac{x^5}{5!} + o(x^5) $$
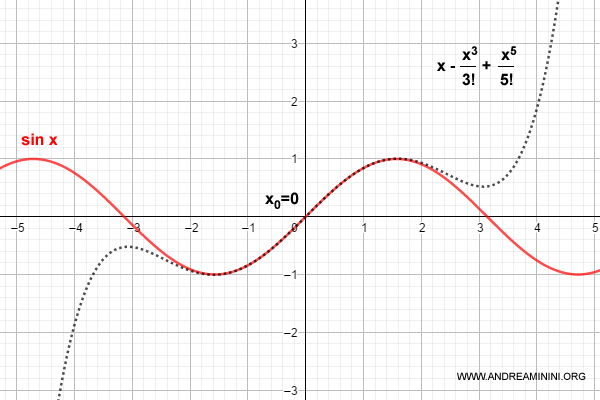
$$ p_5 = x - \frac{x^3}{3!} + \frac{x^5}{5!} + o(x^5) $$
Thus, we have derived the Taylor polynomial.
Note. In this case, since x0 = 0, we are effectively working with a Maclaurin polynomial. However, the same procedure applies for any x0 ≠ 0.
The fifth-degree polynomial provides a fairly good approximation of the sine function in the vicinity of x0 = 0.
How to Generalize the Polynomial for Any n
It’s also possible to generalize the polynomial for any integer n.
Examining the full series - including the zero terms - reveals two clear patterns:
$$ 0 + x + 0 - \frac{x^3}{3!} + 0 + \frac{x^5}{5!} + \dots $$
- The series consists exclusively of terms with odd indices (n = 1, 3, 5), while the even-degree terms vanish.
Note. The first term corresponds to n = 0, so n = 1 is considered the second term.
- The coefficients of the odd-degree terms alternate in sign.
Odd exponents can be generated using the expression 2n + 1.
This construction ensures that the series includes only the odd powers of x:
$$ x - \frac{x^3}{3!} + \frac{x^5}{5!} + \dots $$
To introduce the alternating signs, we multiply each term by (-1)n, which alternates between positive and negative values as n increases from 0 onward.
Thus, the general Taylor or Maclaurin series for the sine function is expressed as:
$$ p_n = x - \frac{x^3}{3!} + \frac{x^5}{5!} + \dots + (-1)^n \cdot \frac{x^{2n+1}}{(2n+1)!} + o(x^{2n+1}) $$
However, a subtle adjustment is required for the little-o notation.
In the full series, the polynomial P2n+1 coincides with the even-index polynomial P2n+2, since all even-degree terms are zero and the series remains unchanged:
$$ P_{2n+1} = P_{2n+2} $$
Therefore, we can express the remainder directly as o(x2n+2).
Hence, the generalized Taylor/Maclaurin series for the sine function is:
$$ p_n = x - \frac{x^3}{3!} + \frac{x^5}{5!} + \dots + (-1)^n \cdot \frac{x^{2n+1}}{(2n+1)!} + o(x^{2n+2}) $$
With this, the Taylor series expansion for the sine function is fully established for any integer n.
And so forth.