Taylor Series
Let f(x) be a function defined on an interval [x0 − δ, x0 + δ] around a point x0, with δ > 0, where f(x) is infinitely differentiable. The function admits a Taylor series expansion if, for every x in [x0 − δ, x0 + δ], the following series converges: $$ \sum_{k=0}^{\infty} \frac{f^{(k)}(x_0)}{k!} (x - x_0)^k $$ and its sum equals f(x): $$ f(x) = \sum_{k=0}^{\infty} \frac{f^{(k)}(x_0)}{k!} (x - x_0)^k $$ for all x in the interval [x0 − δ, x0 + δ].
Purpose and Applications
The Taylor series is derived from the Taylor formula.
It serves to approximate the behavior of a differentiable function f(x) near a point x0 using a polynomial Pn constructed from a numerical series.
The Taylor Theorem
For a function to be expandable into a Taylor series, it must satisfy the following theorem:
A function f(x) can be expressed as a Taylor series centered at x0 if there exists a δ > 0 such that f(x) is infinitely differentiable on [x0 − δ, x0 + δ] and if there is a constant M such that for every n, $$ |f^{(n)}(x)| \le M \quad \forall x \in [x_0 - δ, x_0 + δ]. $$
Proof
The Taylor formula consists of a finite partial sum of order n and a remainder term Rn(x), known as the Peano remainder:
$$ s_n + R_n(x) $$
Including the remainder, the formula represents the function f(x) as:
$$ f(x) = s_n + R_n(x) $$
for every x in the interval (x0 − δ, x0 + δ) where δ > 0.
Note. The Peano remainder Rn(x) quantifies the error when approximating f(x) using the Taylor polynomial. $$ f(x) - s_n = R_n(x) $$
By assumption, f(x) is infinitely differentiable at x0 and bounded by some constant M.
The estimate for the Peano remainder is:
$$ |R_n(x)| \le M \cdot \frac{|x - x_0|^{n+1}}{(n+1)!} $$
Given that (x − x0) < δ:
$$ |R_n(x)| \le M \cdot \frac{|x - x_0|^{n+1}}{(n+1)!} \le M \cdot \frac{\delta^{n+1}}{(n+1)!}. $$
For simplicity, we consider only the upper bound:
$$ |R_n(x)| \le M \cdot \frac{\delta^{n+1}}{(n+1)!}. $$
Taking the limit as n → ∞:
$$ \lim_{n \rightarrow \infty} |R_n(x)| \le \lim_{n \rightarrow \infty} M \cdot \frac{\delta^{n+1}}{(n+1)!}. $$
Since δ > 0, the right-hand limit approaches zero as n → ∞:
$$ \lim_{n \rightarrow \infty} |R_n(x)| \le 0. $$
Hence, the absolute value of the Peano remainder also tends to zero for every x in the interval (x0 − δ, x0 + δ):
$$ \lim_{n \rightarrow \infty} |R_n(x)| = 0. $$
This demonstrates that the partial sums sn(x) approximate the function f(x) within (x0 − δ, x0 + δ):
$$ f(x) = s_n + R_n(x) $$
$$ f(x) - R_n(x) = s_n $$
Therefore, as n → ∞, the Taylor series converges to f(x) in the interval:
$$ \lim_{n \rightarrow \infty} [ f(x) - R_n(x) ] = \lim_{n \rightarrow \infty} s_n $$
$$ f(x) = \lim_{n \rightarrow \infty} s_n $$
$$ f(x) = s_n \quad \text{for } n = \infty $$
In conclusion, the function f(x) can be expanded into a Taylor series around x0 within the interval (x0 − δ, x0 + δ).
A Practical Example
Let’s consider the sine function:
$$ f(x) = \sin x $$
This function is infinitely differentiable, and all of its derivatives are bounded by M ≤ 1.
Thus, we can express it as a Taylor series.
We choose the expansion point x0 = 0.
Note. Any other point could be used, but choosing x0 = 0 simplifies the calculations. When the Taylor series is computed at x0 = 0, it is also known as the Maclaurin series.
We begin with the first term, k = 0:
$$ \frac{f^{(k)}(x_0)}{k!} (x - x_0)^k = \frac{\sin 0}{0!} (x - 0)^0 = 0 $$
Note. f(k)(x0) denotes the k-th derivative of f(x) evaluated at x0. For example, when k = 0, f(0)(x0) = f(x0); when k = 1, f(1)(x0) = f′(x0); when k = 2, f(2)(x0) = f″(x0), and so on.
Next, we compute the second term, k = 1:
$$ \frac{\cos 0}{1!} (x - 0)^1 = x $$
Calculating the third term, k = 2:
$$ \frac{-\sin 0}{2!} (x - 0)^2 = 0 $$
Computing the fourth term, k = 3:
$$ \frac{-\cos 0}{3!} (x - 0)^3 = -\frac{x^3}{3!} $$
Computing the fifth term, k = 4:
$$ \frac{\sin 0}{4!} (x - 0)^4 = 0 $$
Computing the sixth term, k = 5:
$$ \frac{\cos 0}{5!} (x - 0)^5 = \frac{x^5}{5!} $$
Thus, up to k = 5, the Taylor series for the sine function becomes:
$$ \sin x = 0 + x - \frac{x^3}{3!} + 0 + \frac{x^5}{5!} $$
which simplifies to:
$$ \sin x = x - \frac{x^3}{3!} + \frac{x^5}{5!} $$
The polynomial on the right provides an approximation of f(x) around x0 = 0.
The following graph shows the Taylor polynomial (in black) and the function f(x) = sin x (in red) plotted on the Cartesian plane:
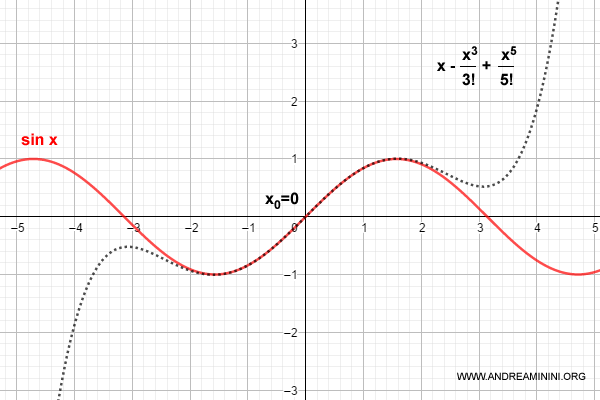
As shown in the graph, the polynomial closely approximates f(x) near x0 = 0.
It’s particularly accurate over the interval from −2 to +2.
Note. If we extended the Taylor series further, for example to k = 10 or k = 20, the polynomial would approximate the sine function even more precisely around x0 = 0, and over a much wider interval than (−2, 2).
And so on.
