Harmonic Series

This is known as the harmonic series: $$ \sum_{k=1}^{\infty} \frac{1}{k} = 1 + \frac{1}{2} + \frac{1}{3} + \frac{1}{4} + \frac{1}{5} + \dots $$

The harmonic series is the sum of the reciprocals of the natural numbers.

Despite its slow growth, the series diverges - a fact that may not be immediately obvious.

A Visual Example

The image below shows the partial sums of the harmonic series as $k$ increases.

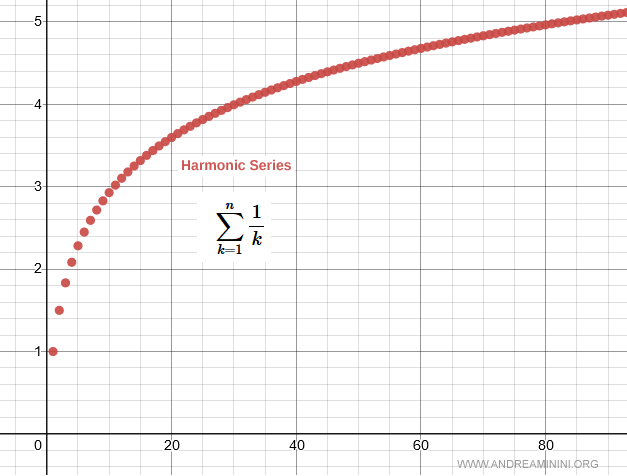
Behavior of the Harmonic Series

The harmonic series diverges as $k \to \infty$.

The individual terms of the series tend to zero as $k \to \infty$:

$$ \lim_{k \rightarrow \infty} \frac{1}{k} = 0 $$

This satisfies the necessary condition for convergence of a series.

Note. While this condition is necessary, it is not sufficient for convergence. It’s a common pitfall to assume otherwise.

In fact, the harmonic series is a well-known example of a divergent series.

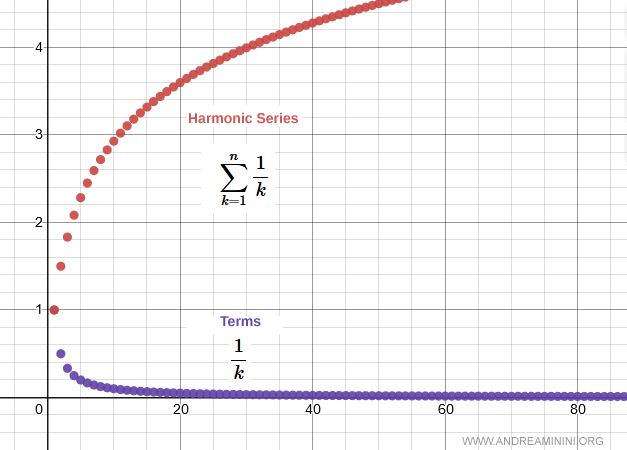
A Proof

To prove divergence, consider the sequence:

$$ a_k = \left(1 + \frac{1}{k} \right)^k $$

This sequence is increasing and converges to a well-known notable limit:

$$ \lim_{k \rightarrow \infty} \left(1 + \frac{1}{k} \right)^k = e $$

So, we can write:

$$ e \ge \left(1 + \frac{1}{k} \right)^k \quad \text{for all } k \in \mathbb{N} $$

Taking the natural logarithm of both sides yields:

$$ \log e \ge \log\left(1 + \frac{1}{k} \right)^k $$

Since $\log e = 1$, we obtain:

$$ 1 \ge k \cdot \log\left(1 + \frac{1}{k} \right) $$

Dividing both sides by $k$ gives:

$$ \frac{1}{k} \ge \log\left(1 + \frac{1}{k} \right) $$

Which is equivalent to:

$$ \frac{1}{k} \ge \log(k+1) - \log(k) $$

This tells us that each term of the harmonic series is greater than or equal to the corresponding term in the logarithmic difference sequence.

Summing both sides from $k = 1$ to $n$:

$$ \sum_{k=1}^{n} \frac{1}{k} \ge \sum_{k=1}^{n} \left[ \log(k+1) - \log(k) \right] $$

So the harmonic series is greater than or equal to a telescoping sum.

This sum simplifies to:

$$ \sum_{k=1}^{n} \left[ \log(k+1) - \log(k) \right] = \log(n+1) - \log(1) = \log(n+1) $$

Hence:

$$ \sum_{k=1}^{n} \frac{1}{k} \ge \log(n+1) $$

Explanation. This is a classic telescoping series: $$ (\log 2 - \log 1) + (\log 3 - \log 2) + \dots + (\log(n+1) - \log n) = \log(n+1) - \log 1 = \log(n+1) $$

Now, taking the limit as $n \to \infty$:

$$ \lim_{n \to \infty} \sum_{k=1}^{n} \frac{1}{k} \ge \lim_{n \to \infty} \log(n+1) = \infty $$

Which implies:

$$ \lim_{n \to \infty} \sum_{k=1}^{n} \frac{1}{k} = \infty $$

This confirms that the harmonic series diverges.

An Alternative Proof

Here’s another approach, based on integration.

For any $x \ge k$, we have:

$$ \frac{1}{x} \le \frac{1}{k} $$

Integrating both sides from $k$ to $k+1$:

$$ \int_k^{k+1} \frac{1}{x} \, dx \le \int_k^{k+1} \frac{1}{k} \, dx $$

Pulling the constant $1/k$ out of the second integral:

$$ \int_k^{k+1} \frac{1}{x} \, dx \le \frac{1}{k} \cdot \int_k^{k+1} dx = \frac{1}{k} $$

Summing from $k = 1$ to $n$ gives:

$$ \sum_{k=1}^n \int_k^{k+1} \frac{1}{x} \, dx \le \sum_{k=1}^n \frac{1}{k} $$

The left-hand side is the integral from 1 to $n+1$:

$$ \int_1^{n+1} \frac{1}{x} \, dx \le \sum_{k=1}^n \frac{1}{k} $$

Explanation. The sum $$ \sum_{k=1}^n \int_k^{k+1} \frac{1}{x} \, dx = \int_1^2 \frac{1}{x} \, dx + \int_2^3 \frac{1}{x} \, dx + \dots + \int_n^{n+1} \frac{1}{x} \, dx $$ represents the area under $1/x$ from $x = 1$ to $x = n+1$, which is $$ \int_1^{n+1} \frac{1}{x} \, dx $$

Evaluating the integral yields:

$$ \log(n+1) - \log(1) = \log(n+1) $$

So:

$$ \log(n+1) \le \sum_{k=1}^n \frac{1}{k} $$

Taking the limit as $n \to \infty$:

$$ \lim_{n \to \infty} \log(n+1) \le \lim_{n \to \infty} \sum_{k=1}^n \frac{1}{k} $$

Since the logarithmic term grows without bound, we conclude:

$$ \infty \le \lim_{n \to \infty} \sum_{k=1}^n \frac{1}{k} $$

By the comparison test, the harmonic series diverges.

And so, the divergence is fully established.