Geometric Series

The geometric series is defined as: $$ \sum_{k=0}^{\infty} x^k = 1 + x + x^2 + \dots + x^k $$

The behavior of a geometric series depends on the value of $x$, referred to as the common ratio.

x ≥ 1: the series diverges
|x| < 1: the series converges
x ≤ -1: the series is undefined or divergent

Determining convergence of a geometric series. When $-1 < x < 1$, the series converges to a finite value: $$ \sum_{k=0}^{\infty} x^k = \frac{1}{1 - x} $$

A practical example

1] Positive common ratio

If the ratio is positive ($x > 0$), the series is a non-negative series.

According to the theorem on non-negative series, such a series either converges to a finite limit or diverges to infinity.

We examine two cases: $x \ge 1$ and $0 < x < 1$.

Case: $x \ge 1$ - the series diverges

Since the terms are all non-negative, the series cannot be undefined. It must either converge or diverge.

To assess convergence, we evaluate the limit of the general term:

$$ \lim_{k \rightarrow \infty} x^k = +\infty \ne 0 $$

The limit does not approach zero, so the series cannot converge.

Therefore, for $x \ge 1$, the series is necessarily divergent:

$$ \lim_{n \rightarrow \infty} \sum_{k=0}^{n} x^k = \pm \infty $$

Example. If $x = 1.1$, the series diverges because the terms do not tend to zero.
graph showing divergence of the geometric series
Even when $x = 1$, the series diverges, since the terms converge to 1 rather than zero.
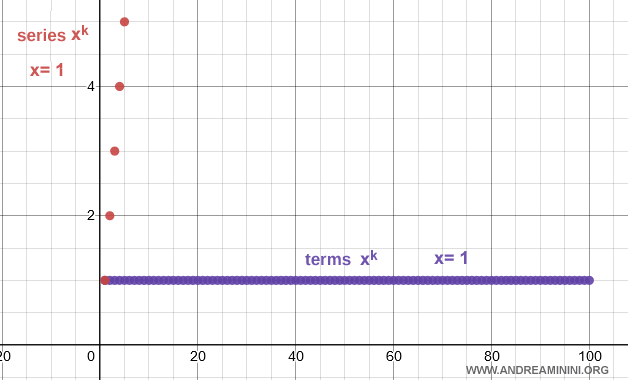
divergent geometric series when x equals 1

Case: $0 \le x < 1$ - the series converges

The series is still non-negative, so again it must either converge or diverge.

Evaluating the general term:

$$ \lim_{k \rightarrow \infty} x^k = 0 $$

This satisfies the necessary (but not sufficient) condition for convergence.

To determine the sum, we use the finite sum formula for geometric series:

$$ 1 + x + x^2 + \dots + x^n = \frac{1 - x^{n+1}}{1 - x} $$

Proof. Observing partial sums, we find: $$ \sum_{k=0}^{n} x^k = \frac{1 - x^{n+1}}{1 - x} $$ We prove this by induction. Base case ($n = 1$): $$ \sum_{k=0}^{1} x^k = 1 + x = \frac{1 - x^2}{1 - x} $$ Assuming the formula holds for $n$: $$ \sum_{k=0}^{n} x^k = \frac{1 - x^{n+1}}{1 - x} $$ Then: $$ \sum_{k=0}^{n+1} x^k = \left( \sum_{k=0}^{n} x^k \right) + x^{n+1} = \frac{1 - x^{n+1}}{1 - x} + x^{n+1} $$ $$ = \frac{1 - x^{n+2}}{1 - x} $$ Thus, the formula holds for all $n \in \mathbb{N}$.

We can now compute the limit:

$$ \lim_{n \rightarrow \infty} \sum_{k=0}^{n} x^k = \lim_{n \rightarrow \infty} \frac{1 - x^{n+1}}{1 - x} $$

Since $x^{n+1} \to 0$ as $n \to \infty$, we obtain:

$$ \frac{1}{1 - x} $$

Therefore, the series converges to $1 / (1 - x)$.

This is a convergent series.

Example. For $x = 0.6$, the series converges because $0.6^k \to 0$ as $k \to \infty$. The sum is: $$ \sum_{k=0}^{\infty} x^k = \frac{1}{1 - 0.6} = 2.5 $$ Below is the graph showing both the series and its terms.
graph of converging geometric series and its terms

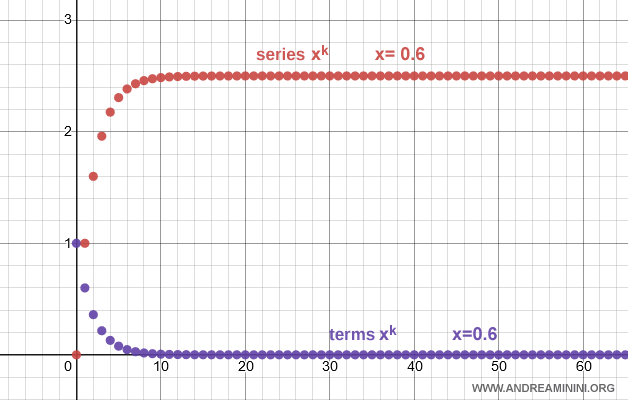
2] Non-positive common ratio

If $x < 0$, we can no longer rely on the non-negative series theorem.

Thus, we cannot rule out the possibility that the series is undefined. A different method is required.

We still use the same identity:

$$ 1 + x + x^2 + \dots + x^n = \frac{1 - x^{n+1}}{1 - x} $$

We consider two separate cases:

Case: $-1 < x \le 0$ - the series converges

Evaluating the limit using the sum formula:

$$ \lim_{n \rightarrow \infty} \sum_{k=0}^{n} x^k = \lim_{n \rightarrow \infty} \frac{1 - x^{n+1}}{1 - x} $$

Since $|x| < 1$, $x^{n+1} \to 0$ as $n \to \infty$:

$$ \frac{1}{1 - x} $$

So the series converges to a finite value.

Example. If $x = -0.8$, the terms approach zero, and although the series oscillates, it converges to: $$ \sum_{k=0}^{\infty} x^k = \frac{1}{1 - (-0.8)} = 0.55 $$ Here is the corresponding graph.
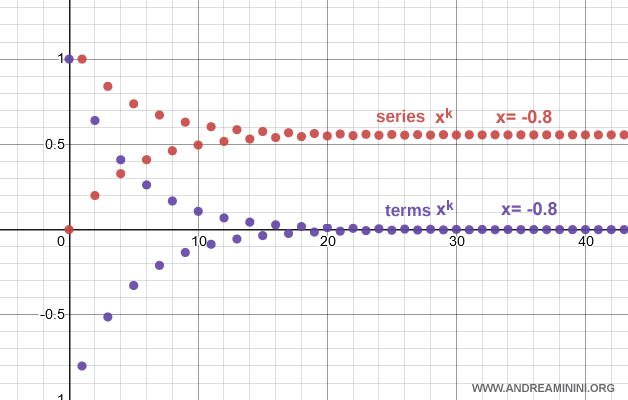
graph of an oscillating but convergent geometric series

Case: $x \le -1$ - the series is undefined

Using the same formula: $$ \sum_{k=0}^{n} x^k = \frac{1 - x^{n+1}}{1 - x} $$

When $x \le -1$, $x^{n+1}$ does not settle to a limit: it alternates and grows without bound depending on whether $n$ is even or odd.

Thus, the limit does not exist, and the series is: $$ \text{undefined} $$

Therefore, for $x \le -1$, the geometric series is considered a non-regular series.

Example. For $x = -1.1$, the series is undefined because the terms do not converge. Both the sequence and the series are oscillatory and unbounded.
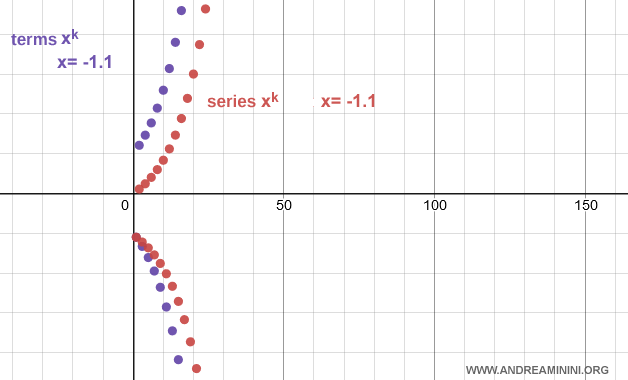
oscillating and undefined geometric series example
The same behavior occurs when $x = -1$.

And so on.