Irregular Series

A series $s_n$ is said to be irregular if the limit of its sequence of partial sums does not exist as $n$ approaches infinity: $$ \lim_{n \rightarrow \infty} s_n = \: \text{ind} $$

Such a series is neither convergent nor divergent in the usual sense.

An illustrative example

Consider the series:

$$ \sum_{n=1}^{\infty} (-1)^n $$

The first few partial sums are:

$$ s_1 = -1 \\ s_2 = -1 + 1 = 0 \\ s_3 = -1 + 1 - 1 = -1 \\ \vdots $$

Thus, the sequence of partial sums is:

$$ s_n = (-1)^n $$

This sequence does not converge, as it oscillates indefinitely between $-1$ and $0$:

$$ \lim_{n \rightarrow \infty} (-1)^n = \: \text{ind} $$

Since the limit is undefined, the series does not converge and does not diverge to infinity. Instead, it is classified as indeterminate.

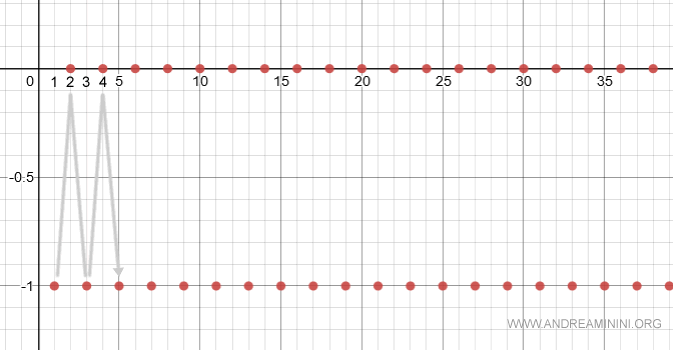
We therefore conclude that the series is irregular.

And so on.