Number Series

A number series s_n is the sum of the first n terms of a given sequence a_n. It's also referred to as the n-th partial sum. $$ s_n = a_1+a_2+...+a_n $$ or, more compactly: $$ s_n = \sum_{k=1}^n a_k $$

The partial sum s_k represents a general term a_k of the number series.

If a sequence contains n terms, then the series will have n corresponding partial sums, one for each k = 1...n.

$$ s_1, s_2, ... , s_n $$

Note. The sequence s_n of partial sums, as n approaches infinity (n→∞), defines the number series associated with the original sequence.

An Example of a Series

Consider the sequence a_n:

$$ a_n = 2n $$

The first n terms of the sequence a_n are:

$$ 2, 4, 6, 8, 10, ... $$

The corresponding partial sums of the series s_n are:

$$ s_1 = 2 $$

$$ s_2 = 2+4 = 6 $$

$$ s_3 = 2+4+6 = 12 $$

$$ s_4 = 2+4+6+8 = 20 $$

$$ s_5 = 2+4+6+8+10 = 30 $$

So the number series s_n of partial sums becomes:

$$ s_1, s_2, s_3, s_4, s_5, ... , s_n $$

$$ 2, 6, 12, 20, 30, ... , s_n $$

The graph below shows the number series (in red) plotted on a Cartesian plane.

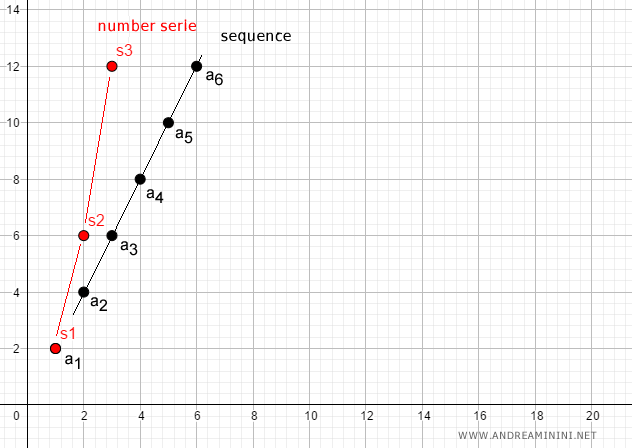
What’s the difference between a series and a sequence? A sequence is an ordered list of individual terms a_k. A series, on the other hand, is the sequence of partial sums s_k formed by summing the terms of a sequence. For instance, the third term of the sequence is a₃ = 6. The third partial sum of the series is s₃ = a₁ + a₂ + a₃ = 2 + 4 + 6 = 12.

Infinite Series

A series is called an infinite series when n = ∞.

$$ \sum_{k=1}^∞ a_k $$

An infinite series is defined as the limit of the partial sums s_n as n approaches infinity:

$$ \lim_{n \rightarrow ∞} s_n $$

Why is the limit of the series important?

The limit determines the convergence behavior of the series - whether it converges, diverges, or is indeterminate.

Note. A series is considered regular if it either converges or diverges. If it does neither, it's known as an irregular series.

Convergence of a Series

The nature (or behavior) of a number series refers to whether the series converges, diverges, or lacks a well-defined limit.

• Convergent series. A series converges if the limit of the partial sums exists and is a finite number. In this case, the sequence s_n tends to a finite value S as n→∞, called the sum of the series: $$ \lim_{n \rightarrow ∞} s_n = S $$

  Note. The sum of the series equals the infinite sum of the terms of the sequence a_n: $$ S = \sum_{k=1}^∞ a_n $$

• Divergent series. A series diverges if the limit of the partial sums tends to positive or negative infinity: $$ \lim_{n \rightarrow ∞} s_n = ±∞ $$
• Indeterminate. A series is indeterminate if the limit does not exist. This is the case for irregular series.

And so on.