Divergent Series

A series $s_n$ is said to diverge if its sequence of partial sums grows without bound as $n$ approaches infinity: $$ \lim_{n \rightarrow \infty} s_n = \infty $$

A concrete example

Consider the series defined by:

$$ s_n = \sum_{k=1}^n \frac{k}{100} $$

The first few partial sums are:

$$ s_1 = \frac{1}{100} = 0.01 \\ s_2 = \frac{1}{100} + \frac{2}{100} = 0.03 \\ s_3 = \frac{1}{100} + \frac{2}{100} + \frac{3}{100} = 0.06 \\ \vdots $$

As $n$ increases, the sum grows larger without ever leveling off:

$$ \lim_{n \rightarrow \infty} \sum_{k=1}^n \frac{k}{100} = \infty $$

Since the partial sums diverge to infinity, the series itself is divergent.

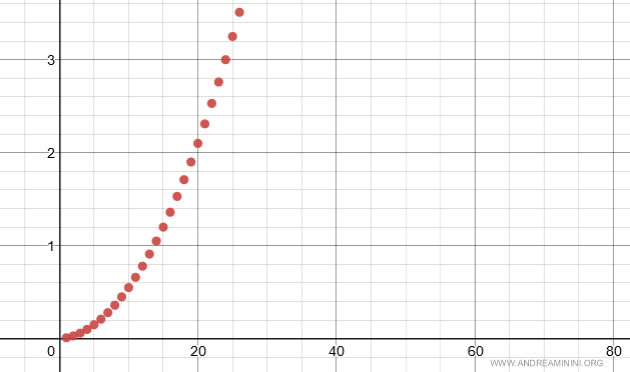
And so on.