Convergent Series

A series s_n is said to converge if its limit as n approaches infinity is a finite number S. $$ \lim_{n \rightarrow \inf} s_n = S $$

A Practical Example

Let’s take a closer look at the Mengoli series:

$$ s_n = \sum_{k=1}^n \frac{1}{k(k+1)} $$

Here are the first few partial sums:

$$ s_1 = \frac{1}{1 \cdot 2} $$

$$ s_2 = \frac{1}{1 \cdot 2} + \frac{1}{2 \cdot 3} $$

$$ s_3 = \frac{1}{1 \cdot 2} + \frac{1}{2 \cdot 3} + \frac{1}{3 \cdot 4} $$

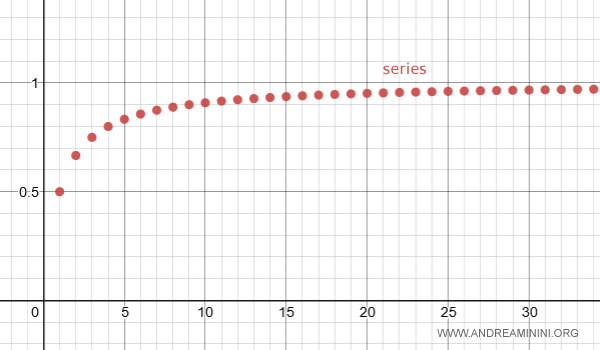
As n approaches infinity, the series s_n converges to 1.

$$ \lim_{n \rightarrow \infty} s_n = \lim_{n \rightarrow \infty} \sum_{k=1}^n \frac{1}{k(k+1)} = 1 $$

Since the limit exists and is finite, we conclude that the series is convergent.

Necessary Condition for Series Convergence

A series s_n can only converge if the general term a_n tends to zero as n approaches infinity.

This condition is necessary, but not sufficient, for convergence.

A Practical Example

Again, consider the Mengoli series:

$$ s_n = \sum_{k=1}^n \frac{1}{k(k+1)} $$

We already know that it converges to 1:

$$ \lim_{n \rightarrow \infty} s_n = 1 $$

The associated sequence a_n is:

$$ a_n = \frac{1}{n(n+1)} $$

Let’s evaluate the first few terms of this sequence:

$$ a_1 = \frac{1}{1 \cdot 2} = \frac{1}{2} $$

$$ a_2 = \frac{1}{2 \cdot 3} = \frac{1}{6} $$

$$ a_3 = \frac{1}{3 \cdot 4} = \frac{1}{12} $$

Clearly, the terms tend to zero as n approaches infinity:

$$ \lim_{n \rightarrow \infty} \frac{1}{n(n+1)} = 0 $$

The graph below compares the behavior of the series and the sequence:

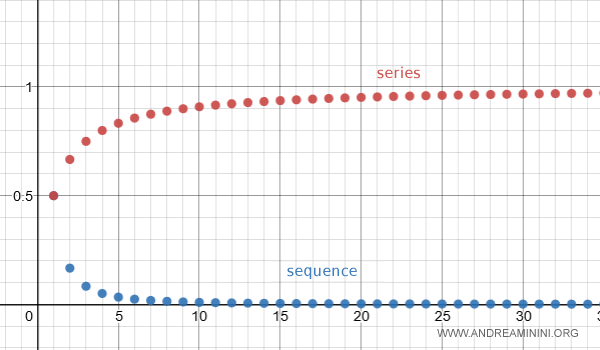
Note. Every convergent series has terms that approach zero. However, the converse doesn’t hold: a sequence whose terms tend to zero does not necessarily produce a convergent series.

Proof

Each term s_n+1 in the series is obtained by adding the next term of the sequence a_n+1 to the previous partial sum s_n:

$$ s_{n+1} = s_{n}+a_{n+1} $$

This implies:

$$ a_{n+1} = s_{n+1} - s_{n} $$

Now, taking the limit as n tends to infinity:

$$ \lim_{n \rightarrow \infty} a_{n+1} = \lim_{n \rightarrow \infty} (s_{n+1} - s_n) = \lim_{n \rightarrow \infty} s_{n+1} - \lim_{n \rightarrow \infty} s_n = S - S = 0 $$

The limit of the sequence is therefore zero. So, convergence is possible - but not guaranteed.

Note. The fact that the sequence tends to zero is only a necessary condition for the series to converge. It's not sufficient. To determine convergence with certainty, we need a criterion that is both necessary and sufficient - such as Cauchy’s criterion.

Cauchy’s Convergence Criterion

A series s_n converges if, for every ε>0, there exists a number v>0 such that for all n>v and any natural number p, $$ \left| \sum_{k=n+1}^{n+p} \right| < \epsilon $$

Cauchy’s convergence criterion provides a necessary and sufficient condition for the convergence of a series.

So, if a series satisfies this condition, it is guaranteed to converge.

Example

Let’s apply this to the series we examined earlier.

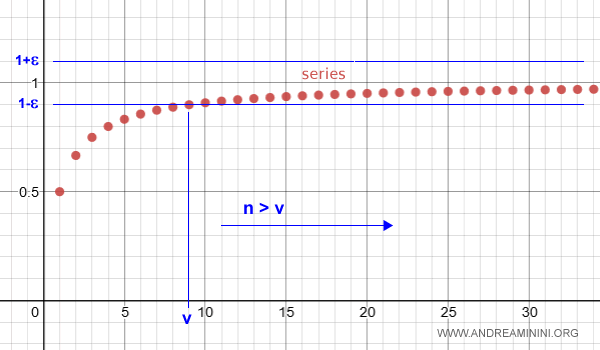
For any ε>0, there exists a threshold v>0 such that for every n>v, the absolute value of the remainder of the series from n+1 to n+p is less than ε.

This confirms that the series is indeed convergent.

Proof

Consider the infinite series:

$$ s_n = \sum_{k=1}^{\infty} a_k $$

The corresponding sequence of partial sums is:

$$ s_1, s_2, s_3, ..., s_n $$

According to Cauchy’s convergence criterion, a sequence converges if and only if for every ε>0, there exists a number v>0 such that for all m, n > v:

$$ |s_m - s_n| <\epsilon $$

Since m > n, we can write:

$$ s_m - s_n <\epsilon $$

Substituting in the expressions for the partial sums:

$$ \sum_{k=1}^m a_k - \sum_{k=1}^n a_k <\epsilon $$

Subtracting the two series leaves only the tail starting from the (n+1)^th term:

$$ \sum_{k=n+1}^m a_k <\epsilon $$

Explanation. The two sums share the first n terms, so the difference is just the tail of the series starting at k = n+1.

Since m > n, we can write m = n + p, where p = m - n:

$$ \sum_{k=n+1}^{n+p} a_k <\epsilon $$

This completes the proof of Cauchy’s convergence criterion for series.

Other Convergence Tests

There are several other useful methods for determining whether a series converges:

• Comparison Test
• Test for Vanishing Terms
• Ratio Test
• Root Test
• Integral Test

...and many more.