Intervals

In mathematics, an interval is a set of consecutive numbers bounded by a lower endpoint (a) and/or an upper endpoint (b), with a< b.

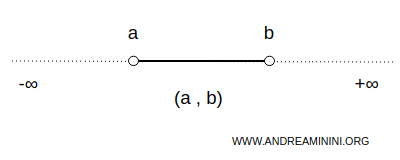
An interval is said to be closed if it includes its endpoints, and open if it excludes them.

An interval may be bounded by two endpoints or extend infinitely in one or both directions.

The difference between the endpoints represents the length of the interval.

$$ b - a $$

The center of the interval is the point:

$$ \frac{a+b}{2} $$

while the radius of the interval is half of its length:

$$ \frac{b-a}{2} $$

Note. In standard mathematical notation, an interval with endpoints "a" and "b" is written using a comma, as in (a,b). However, since in Italy the comma is commonly used as a decimal separator, a semicolon may sometimes be used instead, namely (a;b). For instance, if the endpoints are the decimal numbers 2,5 and 3,4, separating them with a comma would make the interval unclear (2,5,3,4). In such cases, it is preferable either to use the decimal point (2.5,3.4) or to use a semicolon as the separator (2.5;3.4).

The difference between bounded and unbounded intervals

Intervals can be either bounded or unbounded.

• Bounded interval
  A bounded interval is a set of numbers lying between two values, a lower endpoint (a) and an upper endpoint (b), with a< b.
  

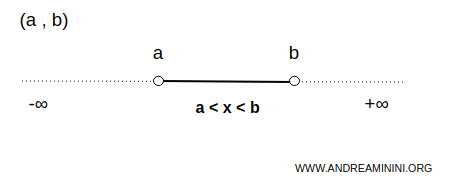
  Example. The set of real numbers between 3 and 10 is a bounded interval of real numbers, where 3 is the lower endpoint and 10 is the upper endpoint. $$ \forall \ x \in (3,10) \Rightarrow \forall \ x \in R \ | \ 3 \lt x \ \lt 10 $$

• Unbounded interval
  An unbounded interval is a set of numbers that extend beyond or precede a given real number x. It may be unbounded above (to the right) or unbounded below (to the left).
  
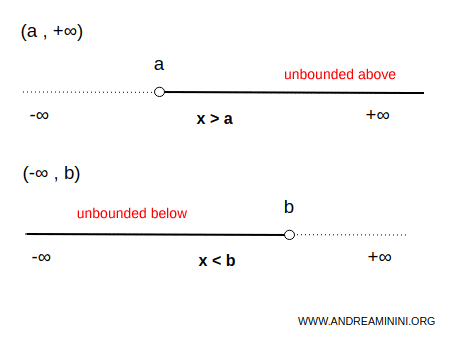
  The symbols $ - \infty $ (minus infinity) and $ + \infty $ (plus infinity) are not numbers and therefore are always excluded from an interval.
  

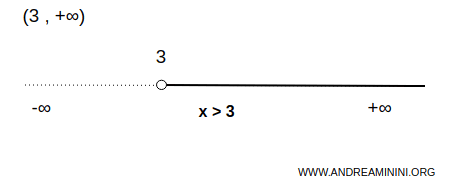
  Example. The set of real numbers greater than 3 is an interval unbounded above and bounded below. Here, 3 is the lower endpoint, while the upper endpoint does not exist. $$ \forall \ x \in (3,+\infty) \Rightarrow \forall \ x \in R \ | \ x \ \gt 3 $$
  
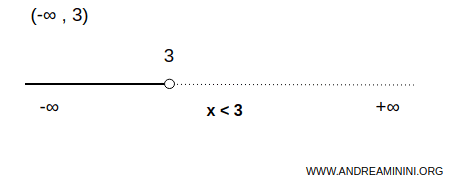
  Example. The set of real numbers less than 3 is an interval unbounded below and bounded above. In this case, 3 is the upper endpoint, while the lower endpoint does not exist. $$ \forall \ x \in (-\infty,3) \Rightarrow \forall \ x \in R \ | \ x \ \lt 3 $$
  

The case of an interval unbounded both below and above

When an interval is unbounded in both directions, it includes all the elements of the reference number set.

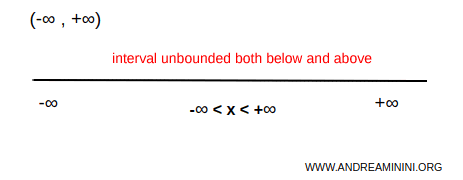
An interval that is unbounded both below and above is simply called unbounded.

Therefore, if an interval is described as unbounded without further qualification, it is understood to be unbounded in both directions.

Example. The set of real numbers (R), unbounded both above and below, is an interval extending to the left and to the right that includes all real numbers. $$ \forall \ x \in (-\infty,+\infty) \Rightarrow \forall \ x \ \in R $$

Open and closed intervals

An interval can be either open or closed.

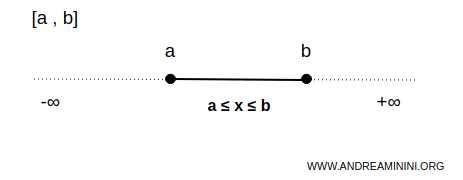
• Closed interval
  An interval is closed if it includes its endpoint. It is denoted by square brackets [ ] on the left and/or right. Graphically, closed endpoints are represented by filled black circles.
  
  

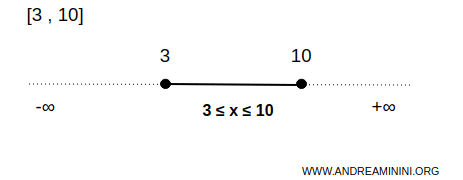
  Example. This bounded interval is closed $$ x \in [3,10] $$ This means that the interval includes all numbers between 3 and 10, including the endpoints 3 and 10. Since both endpoints are closed, they are shown with filled circles.
  

• Open interval
  An interval is open if it does not include its endpoint. It is denoted by round brackets ( ) on the left and/or right. Graphically, open endpoints are represented by hollow circles with a white interior.
  
  

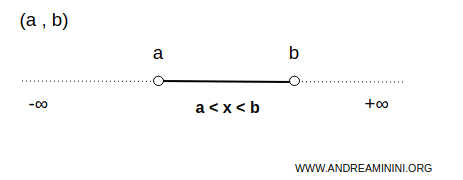
  Example. This bounded interval is open $$ x \in (3,10) $$ This means that the interval includes all numbers between 3 and 10, excluding the endpoints 3 and 10. Since both endpoints are open, they are shown with hollow circles.
  

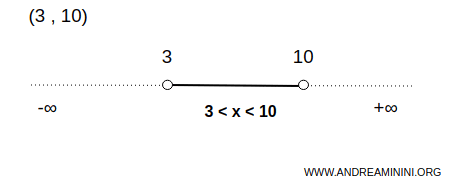
There are many possible combinations of intervals.

For example, an interval may be open on the right and closed on the left, or the other way around, unbounded on the left and closed on the right, and so forth.

The next section presents several practical examples.

Note. In some textbooks, an open interval is written using an alternative notation $$ ]a,b[ \ = (a,b) $$ The underlying concept is exactly the same. Personally, I prefer the use of round brackets.

Practical examples

Example 1

This bounded interval is open on the left and closed on the right.

$$ x \in (3,10] $$

This means that the interval includes all numbers between 3 and 10, excluding the lower endpoint 3 and including the upper endpoint 10.

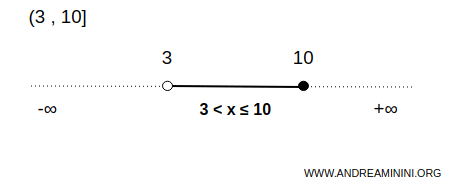
Example 2

This bounded interval is closed on the left and open on the right.

$$ x \in [3,10) $$

This means that the interval includes all numbers between 3 and 10, including the lower endpoint 3 and excluding the upper endpoint 10.

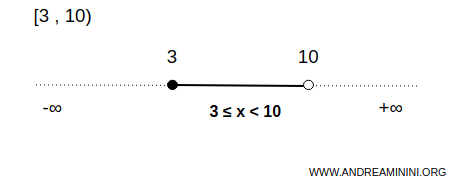
Example 3

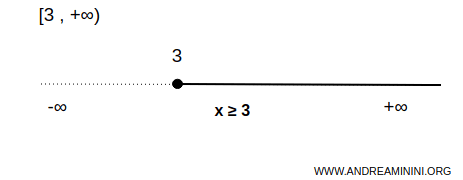
This interval is unbounded above and closed on the left.

$$ x \in [3,+\infty) \Rightarrow \forall \ x \ge 3 $$

This means that the interval includes all numbers greater than or equal to 3. The value 3 is the lower endpoint and is included in the interval. The interval has no upper endpoint.

Note. When the lower or upper endpoint is missing, the infinity symbol (∞) is used. In an interval, an unbounded endpoint (+∞ or -∞) is always open, because ±∞ is only a symbol, not a number, and therefore cannot be included in the interval. For this reason, round brackets are always used at an unbounded endpoint, never square brackets. Some possible examples are (∞,a), (a,∞), (∞,a], [a,∞).

Example 4

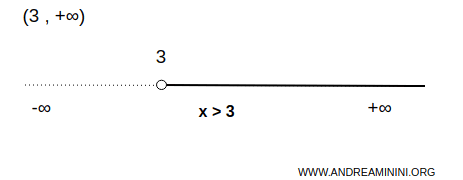
This interval is unbounded above and open at both ends.

$$ x \in (3,+\infty) \Rightarrow \forall \ x \gt 3 $$

This means that the interval includes all numbers greater than 3. The value 3 is the lower endpoint and is not included in the interval. The interval has no upper endpoint.

Example 5

This interval is unbounded below and open on the left and closed on the right.

$$ x \in (-\infty,10] \Rightarrow \forall \ x \ \le 10 $$

This means that the interval includes all numbers less than or equal to 10. The value 10 is the upper endpoint and is included in the interval. The interval has no lower endpoint.

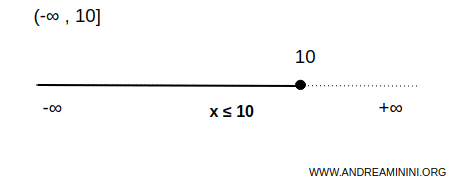
Example 6

This interval is unbounded below and open at both ends.

$$ x \in (-\infty, 10) \Rightarrow \forall \ x \ \lt 10 $$

This means that the interval includes all numbers less than 10. The value 10 is the upper endpoint and is not included in the interval. The interval has no lower endpoint.

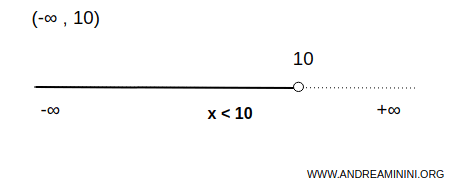
And so on.