Neighborhood of a Point

A neighborhood of a point \( x_0 \) is a set of points that lie sufficiently close to \( x_0 \).

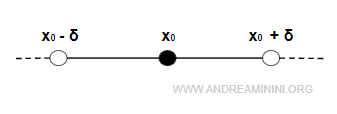
Here \( \delta \) denotes an arbitrary positive real number, introduced as a parameter that controls the size of the neighborhood.

In elementary real analysis, a neighborhood of a point \( x_0 \) is typically represented by a set of points $ I_0 $ that excludes the endpoints of the interval and, depending on the context, may or may not include the point \( x_0 \) itself.

It is therefore important to distinguish between two closely related but conceptually distinct notions.

• Punctured neighborhood
  A punctured neighborhood of $ x_0 $, defined for $ \delta > 0 $, is a neighborhood that excludes the point $ x_0 $. It is given by the union of two open intervals $$  I_{ \delta } (x_0) = (x_0 - \delta, x_0)\ \cup\ (x_0, x_0 + \delta) $$
• Neighborhood containing the point
  A neighborhood of $ x_0 $ that contains the point itself is defined, for $ \delta > 0 $, as the open interval $$  I_{ \delta } (x_0) = (x_0 - \delta, x_0 + \delta)  $$ It can also be expressed in set-theoretic form as $$ I_{ \delta } (x_0) = \{ x \in \mathbb{R} \mid  x_0 - \delta < x < x_0 + \delta \} $$ or, equivalently, as $$ I_{ \delta } (x_0) = \{ x \in \mathbb{R} \mid |x-x_0| < \delta \} $$

Note. In mathematical analysis, when the term “neighborhood of \( x_0 \)” is used without further qualification, it almost always refers to a punctured neighborhood. This convention reflects the fact that, in the study of limits and continuity, the behavior of a function arbitrarily close to a point is of interest, rather than the value of the function at the point itself. This distinction is fundamental to rigorous analysis.

A practical example

Suppose the point x₀ is equal to ten

$$ x_0 = 10 $$

and we fix the value of delta to be two

$$ δ=2 $$

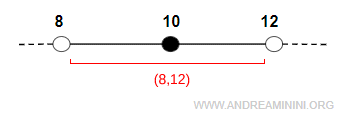
The neighborhood of $ x_0 $ that contains the point is the open interval between eight and twelve

$$ I_0 = (x_0-δ, x_0+δ) $$

$$ I_0 = (10-2, 10+2) $$

$$ I_0 = (8, 12) $$

This is an open interval consisting of all real numbers strictly greater than eight and strictly less than twelve. Since the neighborhood is defined so as to include the point, the value $ x_0 = 10 $ belongs to this neighborhood.

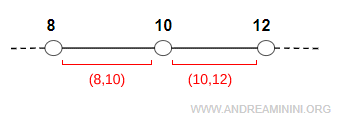
By contrast, the punctured neighborhood of $ 10 $ does not include the point \( x_0 = 10 \). It is not a single open interval, but rather the union of two disjoint open intervals:

$$ I_0 = (x_0 - \delta, x_0)\ \cup\ (x_0, x_0 + \delta) $$

$$ I_0 = (10 - 2, 10)\ \cup\ (10, 10 + 2) $$

$$ I_0 = (8, 10)\ \cup\ (10, 12) $$

In this case, the point $ x_0 = 10 $ does not belong to the neighborhood.

Note. Unless explicitly stated otherwise, a neighborhood need not be symmetric about $ x_0 $. For instance, one may define a neighborhood using two distinct positive real numbers $ \delta_1 \ne \delta_2 $ as $$ (x_0-δ_1, x_0+δ_2) $$ In this case, the point $ x_0 $ is no longer the midpoint of the interval. Some textbooks refer to the symmetric case $ \delta_1 = \delta_2 $ as a neighborhood of radius $ \delta $. The expression “circular neighborhood” is also used in the context of $ \mathbb{R}^2 $ to describe neighborhoods in the plane. To avoid ambiguity, the terms “neighborhood” and “punctured neighborhood” are used here for points on the real line, while circular neighborhood is reserved for neighborhoods in the plane.

Right-hand and left-hand neighborhoods

In many situations, it is useful to analyze the behavior of a function by restricting attention to points lying exclusively to the right or to the left of a given point.

This leads naturally to the notions of right-hand and left-hand neighborhoods.

• Right-hand neighborhood
  The right-hand neighborhood of a point \( x_0 \), denoted by \( I_0^+ \), is the set of real numbers greater than \( x_0 \) and contained in the open interval $ ( x_0, x_0+ \delta ) $, with \( \delta > 0 \). $$ I_0^+ = (x_0, x_0 + \delta) $$
• Left-hand neighborhood
  The left-hand neighborhood of a point \( x_0 \), denoted by \( I_0^- \), is the set of real numbers less than \( x_0 \) and contained in the open interval $ ( x_0- \delta, x_0 ) $, with \( \delta > 0 \). $$ I_0^- = (x_0 - \delta, x_0) $$

These notions play a central role in the study of one-sided limits and in the analysis of the continuity of a function.

For example, if \( x_0 = 2 \) and \( \delta = 0.5 \), then the right-hand neighborhood is \[ I_0^+ = (2, 2.5) \] while the left-hand neighborhood is \[ I_0^- = (1.5, 2) \]

Neighborhood of infinity

In certain contexts, it is useful to consider open intervals that are unbounded above or below.

Such sets are referred to as neighborhoods of infinity.

• Neighborhood of minus infinity
  A neighborhood of minus infinity is the open interval unbounded below that consists of all real numbers less than a fixed real number \( a \).  \[ I(-\infty) = (-\infty, a) = \{ x \in \mathbb{R} \mid x < a \} \]
• Neighborhood of plus infinity
  A neighborhood of plus infinity is the open interval unbounded above that consists of all real numbers greater than a fixed real number \( a \). \[ I(+\infty) = (a, +\infty) = \{ x \in \mathbb{R} \mid x > a \} \]

Whenever the symbol for infinity is used, its sign must always be specified explicitly, since the generic symbol \( \infty \) may refer either to \( -\infty \) or to \( +\infty \).

For example, if \( a = 3 \), then a neighborhood of minus infinity is \[ I(-\infty) = (-\infty, 3) \] whereas a neighborhood of plus infinity is \[ I(+\infty) = (3, +\infty) \] In numerical terms, the number \( -1000 \) belongs to the neighborhood of minus infinity, while the number \( 10 \) belongs to the neighborhood of plus infinity.

Notes

Additional remarks on neighborhoods

• The intersection and the union of two neighborhoods of $ x_0 $ are themselves neighborhoods of $ x_0 $

And so on.