Right-Hand and Left-Hand Limits of a Function

The limit of a function as x approaches x₀ can be evaluated either from the right (x → x₀⁺), meaning we approach x₀ with values greater than x₀. This is known as the right-hand limit:
$$ \lim_{x \rightarrow x_0^+} f(x) $$ or from the left (x → x₀^-), meaning we approach x₀ with values less than x₀. This is called the left-hand limit:
$$ \lim_{x \rightarrow x_0^-} f(x) $$

The right-hand or left-hand limit may be finite or infinite.

At certain points, a function may not possess either a right-hand or left-hand limit.

Example. The logarithmic function f(x) = log(x) is defined only for positive real numbers, i.e. x ∈ (0, +∞). As a result, the limit as x approaches 0 exists solely from the right, that is, as x → 0⁺. There is no left-hand limit as x approaches zero.

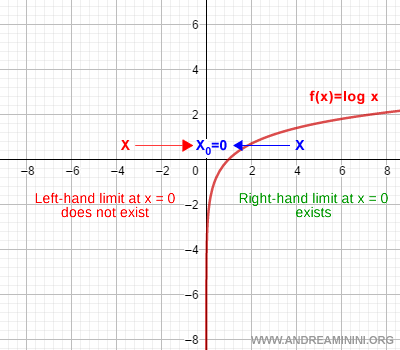
Right-Hand Limit of a Function

Definition of the right-hand limit:

The right-hand limit of a function f(x) as x → x₀⁺ equals l if, for every ε > 0, there exists a δ > 0 such that |f(x) - l| < ε for all x satisfying x₀ < x < x₀ + δ:
$$ \lim_{x \rightarrow x_0^+} f(x) = l $$

Expressed symbolically:

$$ \lim_{x \rightarrow x_0^+} f(x) = l \Leftrightarrow \forall \epsilon>0, \exists \delta>0: |f(x)-l|<\epsilon, \forall x \in (x_0, x_0+\delta) $$

Note. The right-hand limit can also be described using sequences: if we consider a sequence x_n approaching x₀ from the right, then f(x_n) converges to l as n grows large.

Example

The function f(x) = 1/x is undefined at x = 0:

$$ f(x) = \frac{1}{x} $$

We evaluate the limit as x → 0⁺ from the right without ever reaching x = 0:

$$ \lim_{x \rightarrow 0^+} \frac{1}{x} $$

The right-hand limit exists and equals +∞:

$$ \lim_{x \rightarrow 0^+} \frac{1}{x} = +\infty $$

Here’s how this appears on the graph:

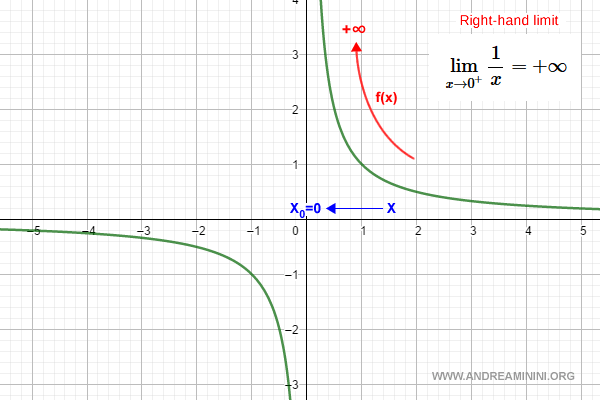
Left-Hand Limit of a Function

Definition of the left-hand limit:

The left-hand limit of a function f(x) as x → x₀^- equals l if, for every ε > 0, there exists a δ > 0 such that |f(x) - l| < ε for all x satisfying x₀ - δ < x < x₀:
$$ \lim_{x \rightarrow x_0^-} f(x) = l $$

Expressed symbolically:

$$ \lim_{x \rightarrow x_0^-} f(x) = l \Leftrightarrow \forall \epsilon>0, \exists \delta>0: |f(x)-l|<\epsilon, \forall x \in (x_0-\delta, x_0) $$

Note. The left-hand limit can also be defined using sequences: if we take a sequence x_n approaching x₀ from the left, then f(x_n) approaches l as n increases.

Example

The function f(x) = 1/x is undefined at x = 0:

$$ f(x) = \frac{1}{x} $$

We evaluate the limit as x → 0^- from the left without ever reaching x = 0:

$$ \lim_{x \rightarrow 0^-} \frac{1}{x} $$

The left-hand limit exists and equals -∞:

$$ \lim_{x \rightarrow 0^-} \frac{1}{x} = -\infty $$

Note. In this case, the limit approaches negative infinity because x approaches zero from the left. Thus, the values of x remain negative, such as x = -0.3, x = -0.1, x = -0.01, and so on.

Here’s how this is represented on the Cartesian plane:

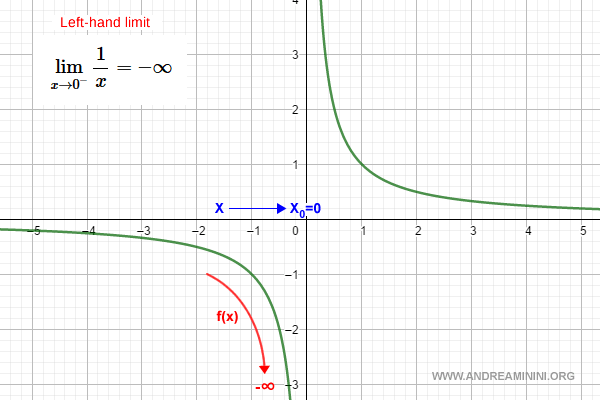
A worked example

Let us examine a concrete example by considering the following function, defined piecewise.

\[
f(x)=
\begin{cases}
x^2 & \text{if } x<2 \\ \\
4x-4 & \text{if } x\ge 2
\end{cases}
\]

Right-hand limit

We begin by analyzing the right-hand limit at \( x=2 \).

\[ \lim_{x\to 2^+} f(x)=4 \]

Because this is a right-hand limit \( x \to 2^+ \), we only consider values of \( x \) that are greater than 2.

In this region, sufficiently close to 2, the function is described by the second branch:

\[ f(x)=4x-4 \]

By definition, saying that \( f(x) \) converges to 4 as \( x\to 2^+ \) means that for every \( \varepsilon>0 \), there exists a right-hand neighborhood of 2 such that

\[ |f(x)-4|<\varepsilon \]

whenever \( x \) belongs to that neighborhood.

Substituting \( f(x)=4x-4 \), we obtain

\[ |(4x-4)-4|<\varepsilon \]

which simplifies to

\[ |4x-8|<\varepsilon \]

Using the standard property of absolute values,

\[ |A|<\varepsilon \quad \Longleftrightarrow \quad -\varepsilon<A<\varepsilon \]

and setting \( A=4x-8 \), we get

\[ -\varepsilon<4x-8<\varepsilon \]

Adding 8 to all terms yields

\[ 8-\varepsilon<4x<8+\varepsilon \]

Dividing by 4 gives

\[ 2-\frac{\varepsilon}{4}<x<2+\frac{\varepsilon}{4} \]

Since we are interested only in values with \( x>2 \), we keep the right-hand portion:

\[ 2<x<2+\frac{\varepsilon}{4} \]

This interval is a right-hand neighborhood of 2.

Writing the condition in terms of \( \delta \), we simply set \( \delta=\frac{\varepsilon}{4} \). Then

\[ 2<x<2+\delta \]

or, equivalently,

\[ 0<x-2<\delta \]

which ensures

\[ 0<x-2<\delta \quad \Longrightarrow \quad |f(x)-4|<\varepsilon \]

Since this construction works for every \( \varepsilon>0 \), we conclude that

\[ \lim_{x\to 2^+} f(x)=4 \]

Left-hand limit

We now turn to the left-hand limit at the same point.

\[
f(x)=
\begin{cases}
x^2 & \text{if } x<2 \\ \\
4x-4 & \text{if } x\ge 2
\end{cases}
\]

We want to verify that

\[ \lim_{x\to 2^-} f(x)=4 \]

Because \( x\to 2^- \), we restrict attention to values with \( x<2 \).

In a left-hand neighborhood of 2, the function is therefore given by the first branch:

\[ f(x)=x^2 \]

By definition, \( f(x) \) converges to 4 as \( x\to 2^- \) if, for every \( \varepsilon>0 \),

\[ |f(x)-4|<\varepsilon \]

whenever \( x \) is sufficiently close to 2 from the left.

Substituting \( f(x)=x^2 \), we obtain

\[ |x^2-4|<\varepsilon \]

This expression is a difference of squares and can be factored as

\[ |x^2-4|=|(x-2)(x+2)|=|x-2|\cdot|x+2| \]

The condition becomes

\[ |x-2|\cdot|x+2|<\varepsilon \]

To control the factor \( |x+2| \), we restrict \( x \) to a small left-hand neighborhood of 2, for example

\[  1<x<2 \]

Adding 2 to each term gives

\[  3<x+2<4 \]

so that

\[ |x+2|<4 \]

This bound allows us to simplify the estimate. Indeed, if \(|x+2|<4 \), then

\[ |x-2|\cdot|x+2|<4|x-2| \]

It is therefore sufficient to require

\[ 4|x-2|<\varepsilon \]

which leads to

\[ |x-2|<\frac{\varepsilon}{4} \]

To ensure that we remain on the left of 2, we must also impose \( x<2 \).

The inequality \(|x-2|<\varepsilon/4 \) is equivalent to

\[ -\frac{\varepsilon}{4}<x-2<\frac{\varepsilon}{4} \]

Adding 2 throughout, we obtain

\[ 2-\frac{\varepsilon}{4}<x<2+\frac{\varepsilon}{4} \]

Combining this with the condition \( x<2 \) yields

\[ 2-\frac{\varepsilon}{4}<x<2 \]

This interval is a left-hand neighborhood of 2.

Consequently, if $ x $ is sufficiently close to 2 from the left, then $ x^2 $ is sufficiently close to 4.

\[ \lim_{x\to 2^-} f(x)=4 \]

Therefore, the left-hand limit is also equal to 4.

And so on.