Cauchy Sequences
A Cauchy sequence is a sequence of real numbers such that, for every ε > 0, there exists an index v with the property that $$ | a_k - a_j | < \epsilon $$ whenever k, j > v.
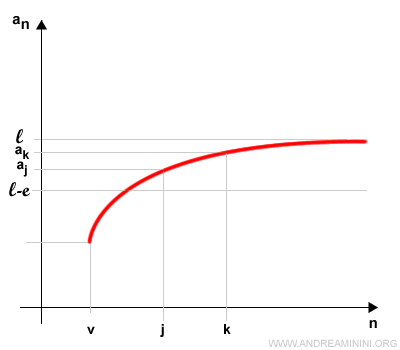
Cauchy sequences are fundamentally connected to the notion of convergence in real analysis.
It can be shown that every Cauchy sequence converges, and conversely, every convergent sequence is a Cauchy sequence.
Cauchy’s Criterion for Convergence
A sequence converges if and only if it is a Cauchy sequence.
Every Convergent Sequence is a Cauchy Sequence
Every convergent sequence is necessarily a Cauchy sequence.
Proof
Suppose the sequence an converges to a finite limit l. Then for any ε > 0, there exists an index v such that for all n > v:
For convenience, let’s choose ε = ε/2:
$$ |a_n - l| < \frac{\epsilon}{2} $$
Take any two indices k, j > v. By convergence:
$$ |a_k - l| < \frac{\epsilon}{2} $$
$$ |a_j - l| < \frac{\epsilon}{2} $$
Adding these inequalities yields:
$$ |a_k - l| + |a_j - l| < \frac{\epsilon}{2} + \frac{\epsilon}{2} $$
$$ |a_k - l| + |a_j - l| < \epsilon $$
Observe that |a_j - l| is equivalent to |l - a_j|. Therefore:
$$ |a_k - l| + |l - a_j| < \epsilon $$
Applying the triangle inequality, |a - b| ≤ |a - c| + |c - b|, gives:
$$ |a_k - a_j| = |(a_k - l) + (l - a_j)| \le |a_k - l| + |l - a_j| < \epsilon $$
This confirms the definition of a Cauchy sequence:
$$ |a_k - a_j| < \epsilon $$
Therefore, every convergent sequence is indeed a Cauchy sequence.
Every Cauchy Sequence is Convergent
Every Cauchy sequence converges.
Combined with the previous theorem, this establishes that a sequence is convergent if and only if it is a Cauchy sequence.
Thus, satisfying one of these conditions guarantees the other.
Note. If a sequence an is not a Cauchy sequence, it either diverges or fails to have a limit (i.e., it is irregular).
Proof
Every Cauchy sequence is bounded. Specifically, for all k, j > v:
$$ | a_k - a_j | < \epsilon $$
Let’s choose ε = 1:
$$ | a_k - a_j | < 1 $$
For any fixed j > v, we can rewrite this inequality as:
$$ a_j - 1 < a_k < a_j + 1 $$
Hence, the terms of the sequence are bounded between aj - 1 and aj + 1:
$$ a_j - 1 < a_k < a_j + 1 $$
Thus:
$$ \min \le a_j - 1 < a_k < a_j + 1 \le \max $$
implying:
$$ \min \le a_k \le \max $$
This demonstrates that a Cauchy sequence is a bounded sequence.
Since it is bounded, by the Bolzano-Weierstrass Theorem, it contains at least one convergent subsequence ank.
Therefore, for some ε > 0:
$$ |a_{n_k} - l| < \epsilon \quad \forall k > v $$
We now need to show that if a Cauchy sequence an contains a convergent subsequence ank converging to l, then the entire sequence converges to the same limit l:
$$ \lim_{n_k \rightarrow \infty} a_{n_k} = l $$
Consider an arbitrary ε > 0, and let ε = ε/2 to check the Cauchy condition:
$$ |a_k - a_j| < \frac{\epsilon}{2} \quad \forall j, k > v $$
We can find an index k such that the convergent subsequence satisfies:
$$ |a_{n_k} - l| < \frac{\epsilon}{2} \quad \forall k > v $$
A sequence an converges if the following condition holds:
$$ \forall \epsilon > 0 \ \exists \ v : |a_n - l| < \epsilon \quad \forall n > v $$
Consider the expression:
$$ |a_n - l + a_{n_k} - a_{n_k}| < \epsilon $$
which can be grouped as:
$$ |(a_n - a_{n_k}) + (a_{n_k} - l)| < \epsilon $$
Applying the triangle inequality |x + y| ≤ |x| + |y| gives:
$$ |a_n - l| \le |a_n - a_{n_k}| + |a_{n_k} - l| < \epsilon $$
Since both terms on the right are less than ε/2 for all k > v:
$$ |a_n - l| \le \frac{\epsilon}{2} + \frac{\epsilon}{2} = \epsilon $$
This shows that:
$$ |a_n - l| < \epsilon \quad \forall n > k $$
Thus, the entire Cauchy sequence an converges to l:
$$ \lim_{n \rightarrow \infty} a_{n} = l $$
Note. Since nk ≥ k and k > v, it follows that nk > v:
$$ \begin{cases} n_k > v \\ \\ n_k \ge k \end{cases} $$
We can combine these into a single inequality:
$$ n_k \ge k > v $$
$$ n_k > v $$
And so on.
