Exercises on Limits of Functions of Two Variables

A selection of solved exercises dealing with limits of functions of two variables.

Exercise 1

We are tasked with evaluating the following limit involving two variables:

$$ \lim_{(x,y) \rightarrow (0,0)} \frac{\sin(x^2+y^2)}{x^2+y^2} $$

As \((x, y)\) approaches \((0, 0)\), the expression takes on the indeterminate form \( \frac{0}{0} \):

$$ \lim_{(x,y) \rightarrow (0,0)} \frac{\sin(x^2+y^2)}{x^2+y^2} = \frac{0}{0} $$

To resolve this, we introduce a change of variables.

Let us define a new variable \( t \) as:

$$ t = x^2 + y^2 $$

This substitution reduces the original two-variable limit to a well-known single-variable limit:

$$ \lim_{t \rightarrow 0} \frac{\sin(t)}{t} $$

It is a standard result that:

$$ \lim_{t \rightarrow 0} \frac{\sin(t)}{t} = 1 $$

Consequently, the limit of the original function \( f(x, y) \) is also equal to 1.

By replacing \( t \) with \( x^2 + y^2 \), we obtain the final result:

$$ \lim_{(x,y) \rightarrow (0,0)} \frac{\sin(x^2+y^2)}{x^2+y^2} = 1 $$

The limit has thus been successfully evaluated.

Exercise 2

Let's find the limit of the following function \( f(x,y) \):

$$ \lim_{(x,y) \rightarrow (0,0)} \frac{x^2y}{x^2+y^2} $$

This limit presents an indeterminate form, 0/0:

$$ \lim_{(x,y) \rightarrow (0,0)} \frac{x^2y}{x^2+y^2} = \frac{0}{0} $$

To analyze it, I'll compare the function \( f(x,y) \) with its absolute value.

Note. For any function \( f(x,y) \), it holds that $$ -| f(x,y) | \le f(x,y) \le | f(x,y) |. $$ If the limit of \( |f(x,y)| \) is zero, then by the squeeze theorem, the limit of \( f(x,y) \) is also zero: $$ \lim_{(x,y) \rightarrow (0,0)} -| f(x,y) | \le \lim_{(x,y) \rightarrow (0,0)} f(x,y) \le \lim_{(x,y) \rightarrow (0,0)} | f(x,y) | $$ $$ 0 \le \lim_{(x,y) \rightarrow (0,0)} f(x,y) \le 0. $$

Thus, we need to determine whether the limit of the absolute value is zero.

$$ \lim_{(x,y) \rightarrow (0,0)} \left| \frac{x^2y}{x^2+y^2} \right| $$

Clearly, the absolute value of the function is non-negative:

$$ 0 \le \left| \frac{x^2y}{x^2+y^2} \right| $$

We can rewrite the expression equivalently as:

$$ 0 \le \lim_{(x,y) \rightarrow (0,0)} |y| \cdot \frac{x^2}{x^2+y^2} $$

Notice that the factor \( \frac{x^2}{x^2+y^2} \) always lies between 0 and 1, since the denominator is greater than or equal to the numerator, and both are positive.

Thus, \( |y| \) is multiplied by a number between 0 and 1.

As a result, the function is bounded above by \( |y| \):

$$ 0 \le |y| \cdot \frac{x^2}{x^2+y^2} \le |y| $$

Taking the limit across the inequality:

$$ \lim_{(x,y) \rightarrow (0,0)} 0 \le \lim_{(x,y) \rightarrow (0,0)} |y| \cdot \frac{x^2}{x^2+y^2} \le \lim_{(x,y) \rightarrow (0,0)} |y| $$

The outer limits clearly tend to zero:

$$ 0 \le \lim_{(x,y) \rightarrow (0,0)} |y| \cdot \frac{x^2}{x^2+y^2} \le 0 $$

By the squeeze theorem, it follows that:

$$ \lim_{(x,y) \rightarrow (0,0)} |y| \cdot \frac{x^2}{x^2+y^2} = 0 $$

and therefore:

$$ \lim_{(x,y) \rightarrow (0,0)} \left| \frac{x^2y}{x^2+y^2} \right| = 0 $$

Consequently, the limit of the original function must also be zero:

$$ \lim_{(x,y) \rightarrow (0,0)} \frac{x^2y}{x^2+y^2} = 0 $$

Explanation. By the squeeze theorem: $$ \lim_{(x,y) \rightarrow (0,0)} - \left| \frac{x^2y}{x^2+y^2} \right| = 0 \le \lim_{(x,y) \rightarrow (0,0)} \frac{x^2y}{x^2+y^2} \le \lim_{(x,y) \rightarrow (0,0)} \left| \frac{x^2y}{x^2+y^2} \right| = 0 $$

Alternative Approach

We can also compute the limit by switching to polar coordinates.

\[ \lim_{(x,y) \to (0,0)} \frac{x^2 y}{x^2 + y^2} \]

Why use polar coordinates? Polar coordinates are particularly helpful when studying limits as \((x,y)\) approaches \((0,0)\), because they simplify the expression and make it easier to track how the function depends on the distance from the origin.

The change to polar coordinates is given by:

\[ x = \rho \cos \theta \]

\[ y = \rho \sin \theta \]

where \(\rho\) represents the distance from the origin (\( \rho = \sqrt{x^2 + y^2} \)) and \(\theta\) is the angle relative to the positive \(x\)-axis.

Substituting these into the function yields:

\[ \frac{x^2 y}{x^2 + y^2} = \frac{(\rho \cos\theta)^2 (\rho \sin\theta)}{(\rho \cos\theta)^2 + (\rho \sin\theta)^2} \]

Expanding and simplifying:

\[ \frac{x^2 y}{x^2 + y^2} = \frac{\rho^2 \cos^2\theta \cdot \rho \sin\theta}{\rho^2 \cos^2\theta + \rho^2 \sin^2\theta} \]

\[ = \frac{\rho^3 \cos^2\theta \sin\theta}{\rho^2 (\cos^2\theta + \sin^2\theta)} \]

By the Pythagorean identity, \( \cos^2\theta + \sin^2\theta = 1 \), so this simplifies to:

\[ \frac{x^2 y}{x^2 + y^2} = \frac{\rho^3 \cos^2\theta \sin\theta}{\rho^2} \]

Thus, the function becomes:

\[ \frac{x^2 y}{x^2 + y^2} = \rho \cos^2\theta \sin\theta \]

We now take the limit:

\[ \lim_{\rho \to 0} \rho \cos^2\theta \sin\theta \]

Since \(\theta\) is held constant as \(\rho\) tends to zero, \( \cos^2\theta \sin\theta \) acts as a constant.

Thus, the product tends to zero as \(\rho\) goes to zero:

\[ \cos^2\theta \sin\theta \cdot \lim_{\rho \to 0} \rho = 0 \]

In conclusion, the limit of the two-variable function is:

\[ \lim_{(x,y)\to(0,0)} \frac{x^2 y}{x^2 + y^2} = 0 \]

Exercise 3

In this exercise, we examine the limit of a function of two variables:

\[ \lim_{(x,y)\to(0,0)} \frac{xy}{x^2 + y^2} \]

Our goal is to determine whether this limit exists and, if so, to what value it converges.

Observing the function, we immediately see that the numerator, \(xy\), can take positive, negative, or zero values, while the denominator is always positive, since \(x^2 + y^2 > 0\) whenever \((x,y) \ne (0,0)\).

\[ f(x,y) = \frac{xy}{x^2 + y^2} \]

Hence, the function is defined everywhere except at the origin, \((0,0)\).

Solution 1

A reliable way to check whether a limit exists is to evaluate it along several different paths approaching \((0,0)\). If the results differ along different paths, then the limit does not exist.

A] Case 1: Along the line \(y = 0\)

Let’s set y = 0 and analyze the limit along this path:

\[ f(x,0) = \frac{x \cdot 0}{x^2 + 0} = 0 \]

So along \(y = 0\), the limit of the function is zero:

\[ \lim_{x \to 0} f(x,0) = 0 \]

B] Case 2: Along the line \(y = x\)

Next, substitute \(y = x\) into the function:

\[ f(x,x) = \frac{x \cdot x}{x^2 + x^2} = \frac{x^2}{2x^2} = \frac{1}{2} \]

Thus, along the path \(y = x\), we find:

\[ \lim_{x \to 0} f(x,x) = \frac{1}{2} \]

From this, we conclude that the limit does not exist because we obtained different values along two distinct paths:

• along \(y = 0\) → \(0\)
• along \(y = x\) → \(\frac{1}{2}\)

If the limit varies depending on the path, then it does not exist.

Solution 2

Since we’re taking the limit as we approach the origin, another effective approach is to use polar coordinates for the variables x and y:

\[ x = \rho \cos\theta \]

\[ y = \rho \sin\theta \]

Note. Polar coordinates are particularly convenient when evaluating limits at the origin (0,0). If you wish to compute a limit at a different point using polar coordinates, you first need to translate the coordinate system so that the point of interest becomes the new origin.

Substituting these into the function gives:

\[ f(x,y) = \frac{xy}{x^2 + y^2} = \frac{(\rho \cos\theta)(\rho \sin\theta)}{(\rho \cos\theta)^2 + (\rho \sin\theta)^2} \]

\[ f(x,y) = \frac{\rho^2 \cos\theta \sin\theta}{\rho^2 (\cos^2\theta + \sin^2\theta)} \]

\[ f(x,y) = \frac{\rho^2 \cos\theta \sin\theta}{\rho^2 \cdot 1} \]

\[ f(x,y) = \cos\theta \sin\theta \]

Therefore, the limit becomes:

\[ \lim_{\rho \to 0} f(x,y) = \cos\theta \sin\theta \]

It’s immediately clear that the expression \(\cos\theta \sin\theta\) does not depend on \(\rho\), but rather on the angle \(\theta\).

Since \(\theta\) represents the direction of approach, the limit depends on the path taken. Consequently, the limit does not exist because it yields different values along different directions.

Exercise 4

We wish to analyze the limit of the following function of two variables as \((x,y)\) approaches the origin \((0,0)\):

\[ \lim_{(x,y)\to(0,0)} \frac{xy^2}{x^2 + y^4} \]

The function is:

\[ f(x,y) = \frac{xy^2}{x^2 + y^4} \]

The numerator \( xy^2 \) clearly approaches zero as \(x\) and \(y\) tend to zero.

The denominator \( x^2 + y^4 \) is always positive except at \((0,0)\), where it equals zero. Thus, the function is undefined precisely at the origin.

Hence, the limit takes on the indeterminate form \(\frac{0}{0}\) and requires further investigation.

Solution 1

Let’s attempt to compute the limit along several different paths.

A] Case 1: Along the line \(x = 0\)

We set \(x = 0\) to examine the behavior along the y-axis:

\[ f(0,y) = \frac{0 \cdot y^2}{0 + y^4} = 0 \]

It’s evident that along this path, the limit of the function is zero:

\[ \lim_{(x,y)\to(0,0)} f(0,y)=0 \]

B] Case 2: Along the line \(y = 0\)

Now, we set \(y = 0\) to study the function along the x-axis:

\[ f(x,0) = \frac{x \cdot 0}{x^2 + 0} = 0 \]

Again, we see that along this path, the limit is zero:

\[ \lim_{(x,y)\to(0,0)} f(x,0)=0 \]

C] Case 3: Along the line \(y = x\)

Let’s check what happens along the diagonal path \(y = x\):

\[ f(x,x) = \frac{x \cdot x^2}{x^2 + x^4} = \frac{x^3}{x^2(1 + x^2)} = \frac{x}{1 + x^2} \]

Along this path, as \(x \to 0\), the limit is zero:

\[ \lim_{x \to 0} \frac{x}{1 + x^2} = 0 \]

Is this enough to conclude that the overall limit is zero? Absolutely not!

There are infinitely many paths to approach the point \((0,0)\) - not just straight lines, but also curves of various shapes.

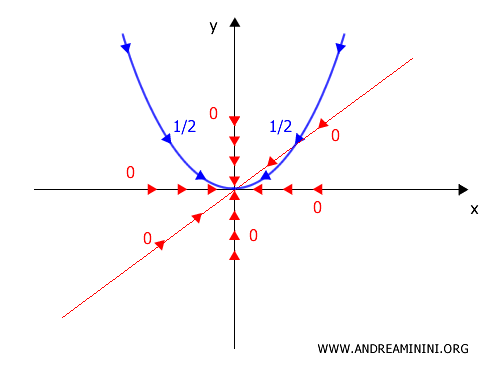
D] Case 4: Along the parabola \(x = y^2\)

Let’s see what happens along the curve \(x = y^2\):

\[ f(y^2, y) = \frac{y^2 \cdot y^2}{(y^2)^2 + y^4} = \frac{y^4}{y^4 + y^4} = \frac{y^4}{2y^4} = \frac{1}{2} \]

Along this trajectory, the limit is not zero but rather \(\frac{1}{2}\):

\[ \lim_{(x,y)\to(0,0)} f(y^2,y)=\frac{1}{2} \]

Since we have identified paths yielding different limit values, the overall limit cannot exist.

Solution 2

Because the limit is taken as we approach the origin, another effective technique is to convert to polar coordinates.

\[ \lim_{(x,y)\to(0,0)} \frac{xy^2}{x^2 + y^4} \]

We substitute Cartesian coordinates \((x,y)\) with polar coordinates \( x = \rho \cos \theta \) and \( y = \rho \sin \theta \):

\[ \lim_{\rho \to 0} \frac{(\rho \cos \theta)\cdot (\rho \sin \theta)^2}{(\rho \cos \theta)^2 + (\rho \sin \theta)^4} \]

\[ \lim_{\rho \to 0} \frac{\rho \cos \theta \cdot \rho^2 \sin^2 \theta}{\rho^2 \cos^2 \theta + \rho^4 \sin^4 \theta} \]

\[ \lim_{\rho \to 0} \frac{\rho^3 \cos \theta \sin^2 \theta}{\rho^2 \cos^2 \theta + \rho^4 \sin^4 \theta} \]

\[ \lim_{\rho \to 0} \frac{\rho \cos \theta \sin^2 \theta}{\cos^2 \theta + \rho^2 \sin^4 \theta} \]

\[ \lim_{\rho \to 0} \rho \cdot \frac{\cos \theta \sin^2 \theta}{\cos^2 \theta + \rho^2 \sin^4 \theta} \]

In this case, the limit is not independent of \(\theta\).

For instance, if \(\theta\) is kept constant, the path is a straight line, and the limit as \(\rho \to 0\) is zero:

\[ \lim_{\rho \to 0} \rho \cdot \frac{\cos \theta \sin^2 \theta}{\cos^2 \theta + \rho^2 \sin^4 \theta} = 0 \]

Note. This occurs because both \(\cos \theta \sin^2 \theta\) and \(\cos^2 \theta\) are constant values that depend only on \(\theta\), while \(\rho^2 \sin^4 \theta\) tends to zero. Thus, the ratio \(\frac{\cos \theta \sin^2 \theta}{\cos^2 \theta + \rho^2 \sin^4 \theta}\) remains bounded, and multiplying it by \(\rho\) forces the entire expression to zero as \(\rho \to 0\).

However, suppose we choose a curved trajectory where \(\cos \theta(\rho) = k \rho\) with \(k \ne 0\). Then the denominator becomes of order \((k \rho)^2 + \rho^2 \sin^4 \theta\), while the numerator is of order \(\rho \cdot (k \rho) \sin^2 \theta\):

\[ \lim_{\rho \to 0} \rho \cdot \frac{(k \rho) \cdot \sin^2 \theta}{(k \rho)^2 + \rho^2 \sin^4 \theta} \]

If \(\cos \theta(\rho) = k \rho\), then \(\sin \theta(\rho) = \sqrt{1 - \cos^2 \theta(\rho)} = \sqrt{1 - (k \rho)^2}\).

Therefore, \(\sin^2 \theta(\rho) = 1 - (k \rho)^2\), which tends to 1 as \(\rho \to 0\).

\[ \lim_{\rho \to 0} \rho \cdot \frac{(k \rho) \cdot 1}{(k \rho)^2 + \rho^2 \cdot 1} \]

\[ \lim_{\rho \to 0} \rho \cdot \frac{k \rho}{k^2 \rho^2 + \rho^2} \]

\[ \lim_{\rho \to 0} \frac{k \rho^2}{\rho^2 (k^2 + 1)} \]

\[ \lim_{\rho \to 0} \frac{k}{k^2 + 1} = \frac{k}{k^2 + 1} \]

So along this curved path, the limit approaches the finite non-zero value \( \frac{k}{k^2 + 1} \).

In conclusion, because along straight paths (constant \(\theta\)) the limit is zero, but along the curved path \(\cos \theta(\rho) = k \rho\) it approaches a non-zero finite value, we deduce that the overall limit of the function does not exist as \((x,y)\) approaches \((0,0)\).

And so on.