Theorem on the Preservation of Sign for the Limit of a Function

Let f(x) be a function defined and continuous in a neighborhood of the point x₀. If f(x₀) > 0, then there exists a number δ > 0 such that f(x) > 0 for all x in the interval (x₀ - δ, x₀ + δ).

Example

Consider the function:

$$ f(x) = \frac{1}{x} $$

At the point x₀ = 2, the function evaluates to f(x₀) = 0.5:

$$ f(2) = 0.5 $$

Let’s look at a neighborhood around x₀ = 2 with δ = 0.2:

$$ (x_0 - \delta, \, x_0 + \delta) $$

$$ (2 - 0.2, \, 2 + 0.2) $$

$$ (1.8, \, 2.2) $$

Within the interval (1.8, 2.2), the function f(x) remains strictly positive:

$$ f(1.8) = \frac{1}{1.8} = 0.55 \\ f(2.2) = \frac{1}{2.2} = 0.45 $$

Graphically, this can be illustrated as follows:

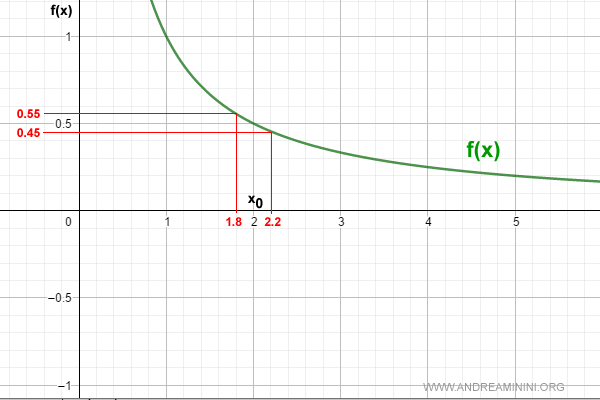
Note. For any x₀ such that f(x₀) > 0, it is always possible to find some δ > 0 that defines a neighborhood in which f(x) > 0 for all x ∈ (x₀ - δ, x₀ + δ). 

Proof

Since the function is positive at the point x₀:

$$ f(x_0) > 0 $$

We choose:

$$ \epsilon = \frac{f(x_0)}{2} $$

By the definition of the limit, there exists a δ > 0 such that:

$$ |f(x) - f(x_0)| < \epsilon $$

which is equivalent to:

$$ |f(x) - f(x_0)| < \frac{f(x_0)}{2} $$

This leads to the double inequality:

$$ -\frac{f(x_0)}{2} < f(x) - f(x_0) < \frac{f(x_0)}{2} $$

Adding f(x₀) to all sides gives:

$$ f(x_0) - \frac{f(x_0)}{2} < f(x) < f(x_0) + \frac{f(x_0)}{2} $$

Since f(x₀) - f(x₀)/2 simplifies to f(x₀)/2:

$$ f(x_0) - \frac{f(x_0)}{2} = \frac{f(x_0)}{2} $$

And because f(x₀) > 0, it follows that f(x₀)/2 > 0. Therefore, f(x) remains strictly positive in the neighborhood:

$$ 0 < \frac{f(x_0)}{2} < f(x) < \frac{3f(x_0)}{2} $$

Alternative proof

Suppose that the function f(x) has a finite limit $ l \ne 0 $ as $ x \to x_0 $.

$$ \lim_{x \to x_0} f(x) = l $$

By the definition of a finite limit, for every $ \varepsilon > 0 $ there exists a neighborhood of $ x_0 $ such that

$$ | f(x) - l | < \varepsilon $$

By the basic property of absolute values, this inequality is equivalent to

$$ l - \varepsilon < f(x) < l + \varepsilon $$

Choosing $ \varepsilon = | l | $, we obtain

$$ l - | l | < f(x) < l + | l | $$

We now distinguish two cases

• If the limit is positive ( $ l > 0 $ ), then $$ 0 < f(x) < 2l $$  hence the function is strictly positive, $ f(x) > 0 $, in a neighborhood $ I $ of $ x_0 $
• If the limit is negative ( $ l < 0 $ ), then $$ 2l < f(x) < 0 $$  hence the function is strictly negative, $ f(x) < 0 $, in a neighborhood $ I $ of $ x_0 $

This establishes the claim.

Converse theorem

Proof

Argue by contradiction. Assume that f(x) is nonnegative, $ f(x) \ge 0 $, in a neighborhood $ I(x_0) $, while its limit is negative ( $ l < 0 $ ).

By the theorem on the permanence of sign, if $ l < 0 $, then there exists a neighborhood $ I'(x_0) $ in which

$$ f(x) < 0 $$

Consider the intersection \( I(x_0) \cap I'(x_0) \), which is still a neighborhood of $ x_0 $. Within this neighborhood, the inequalities

\[  f(x) \ge 0 \quad \text{and} \quad f(x) < 0 \]

would have to hold simultaneously.

This is impossible, since a function cannot be both nonnegative and negative at the same point.

Therefore, the assumption \( l < 0 \) is untenable, and the limit must satisfy

\[ l \ge 0 \]

This completes the proof.

Note The second statement is proved analogously. Assume \( f(x) \le 0 \) in a neighborhood of \( x_0 \), then rule out by contradiction the possibility \( l > 0 \), again invoking the theorem on the permanence of sign.

And so on.