Limit of the Product of a Bounded Sequence and a Vanishing Sequence
Consider two sequences, an and bn. If an is bounded and bn is a vanishing sequence (i.e. it converges to zero), then the limit of their product, an·bn, also converges to zero. $$ \lim_{n \rightarrow \infty } a_n \cdot b_n = 0 $$
A Practical Example
Let’s look at the following two sequences:
$$ a_n = \frac{n+1}{n} $$
$$ b_n = \frac{1}{n} $$
The first sequence, an, is bounded, while the second sequence, bn, is vanishing.
$$ \lim_{n \rightarrow \infty } a_n = \lim_{n \rightarrow \infty } \frac{n+1}{n}= 1 $$
$$ \lim_{n \rightarrow \infty } b_n = \lim_{n \rightarrow \infty } \frac{1}{n} = 0 $$
Note. A sequence is bounded if there exists some number M>0 such that an<M for all n>0. A sequence bn is said to be vanishing if it converges to zero as n approaches infinity.
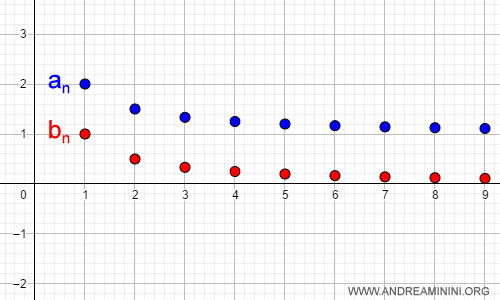
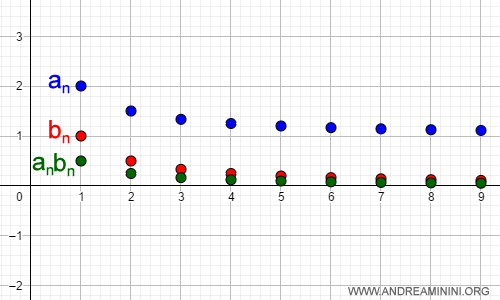
The limit of the product sequence an·bn also converges to zero.
$$ \lim_{n \rightarrow \infty } a_n \cdot b_n = 1 \cdot 0 = 0 $$
Let’s verify this result step by step.
First, compute the product an·bn and then take the limit:
$$ \lim_{n \rightarrow \infty } a_n \cdot b_n $$
$$ \lim_{n \rightarrow \infty } \frac{n+1}{n} \cdot \frac{1}{n} $$
$$ \lim_{n \rightarrow \infty } \frac{n+1}{n^2} = \frac{\infty}{\infty} $$
This limit is an indeterminate form ∞/∞.
To resolve it, we can apply L’Hôpital’s Rule:
$$ \lim_{n \rightarrow \infty } \frac{D[n+1]}{D[n^2]} $$
$$ \lim_{n \rightarrow \infty } \frac{1}{2n} = 0 $$
So, the limit of the product sequence an·bn is indeed zero.
Therefore, the sequence an·bn converges to zero as n→∞.
Proof and Explanation
Let’s consider a bounded sequence an and a vanishing sequence bn.
Since an is bounded, there exists some number M>0 such that:
$$ | a_n | \le M $$
Multiplying both sides of this inequality by |bn| yields:
$$ | a_n | \cdot |b_n| \le M \cdot |b_n| $$
Rewriting this gives:
$$ -M \cdot |b_n| \le a_n \cdot b_n \le M \cdot |b_n| $$
Because bn is vanishing, it approaches zero as n grows without bound.
$$ -M \cdot |0| \le a_n \cdot b_n \le M \cdot 0 $$
By the Squeeze Theorem, the sequence an·bn must also converge to zero.
And that completes the proof.
