Weierstrass’ Theorem

If a function f(x) is continuous over a closed and bounded interval [a,b], then it attains both a minimum value m = f(x₁) and a maximum value M = f(x₂), satisfying $$ f(x_1) \le f(x) \le f(x_2) \:\:\: \forall x \in [a,b] $$

The points \( x_1 \) and \( x_2 \) in the interval \([a,b]\) are referred to as the points of absolute minimum and absolute maximum, respectively.

Weierstrass’ theorem offers a sufficient but not necessary condition for the existence of absolute extrema.

In other words, even if a function isn’t continuous, or the interval isn’t closed and bounded, it’s still possible for absolute maxima or minima to exist - but there’s no guarantee.

Note. More generally, the theorem extends to functions of several variables (for instance, \( f(x,y) \)), provided the domain is closed and bounded* (i.e. compact) and the function remains continuous on that domain.

A Practical Example

Consider the following function:

$$ f(x) = \frac{1}{x} $$

This function is unbounded on the interval (0,5] because it has no finite upper limit, and therefore cannot have a maximum value (M).

Likewise, it’s unbounded on the interval [5,+∞) because, although it tends towards zero (acting as a lower limit), there’s no value of x such that f(x)=0. So it doesn’t possess a minimum value (m) either.

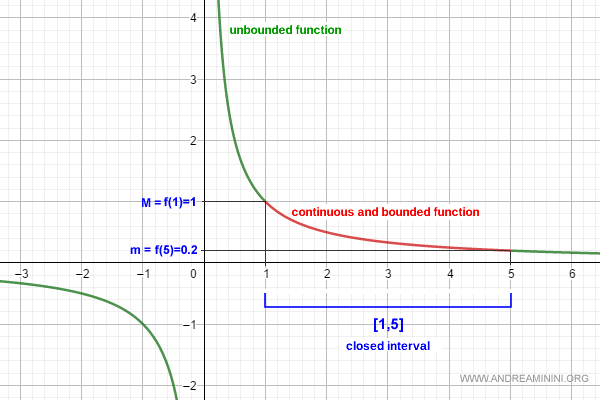
However, if we restrict the function to the closed interval [1,5], f(x) becomes a bounded function.

$$ 0.2 \le f(x) \le 1 \:\:\: \forall x \in [1,5] $$

In this scenario, there are two points, \( x_1 \) and \( x_2 \), within the interval [a,b] where the function attains its minimum and maximum values.

$$ M = f(1) = 1 $$

$$ m = f(5) = 0.2 $$

Note. In this case, the minimum and maximum values occur at the endpoints of the closed interval [a,b]. However, that’s not always the case; in other situations, the absolute minimum or maximum might lie inside the interval. I mention this because it’s a common source of confusion.

The Proof Explained

Let’s examine a function f(x) defined over a closed interval [a,b], and suppose it attains a maximum value M.

$$ M = sup(f(x):x \in [a,b]) $$

Example. This graph depicts the cosine function over the interval [-1,1]. The function reaches its maximum at \( x_0 = 0 \), where f(x) equals M = 1.

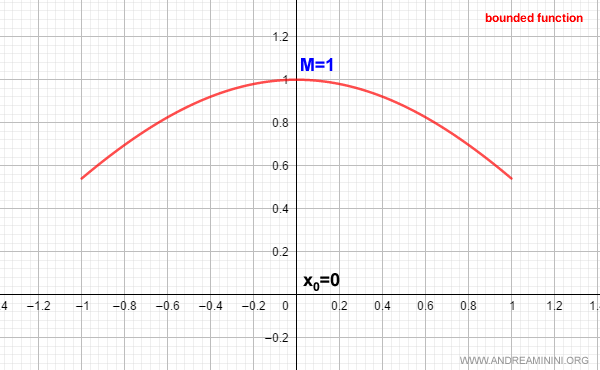
Since an upper bound M exists, we can find a sequence \( x_n \) whose function values approach this maximum:

$$ \lim_{n \rightarrow \infty;} f(x_n) = M $$

Two possibilities arise:

1. M is infinite
   If \( M = +\infty \), then for every \( n \in \mathbb{N} \), there’s an \( x_n \) in [a,b] such that $$ f(x_n) > n $$. Therefore, the sequence diverges to infinity: $$ M = \lim_{n \rightarrow \infty;} f(x_n) = \infty $$
2. M is finite
   If \( M < +\infty \), then for each \( n \in \mathbb{N} \), there’s an \( x_n \) in [a,b] such that $$ M - \frac{1}{n} < f(x_n) \le M $$. Thus, the sequence converges to a finite value: $$ M = \lim_{n \rightarrow \infty;} f(x_n) = f(x_0) $$

The next step is to determine whether M is finite or infinite.

Because [a,b] is bounded, the sequence \( x_n \) is bounded as well. Therefore, by the Bolzano-Weierstrass theorem, there exists a subsequence \( x_{nk} \) that converges to some point within [a,b].

Example. Here’s an example of a convergent subsequence.

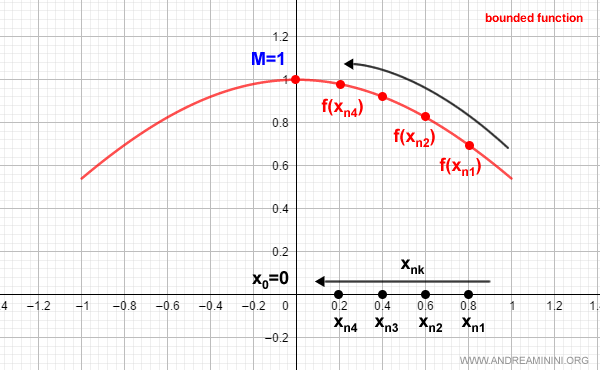
Consider a subsequence \( x_{nk} \) converging to the point \( x_0 \) in [a,b]:

$$ \lim_{n \rightarrow \infty;} x_{nk} = x_0 $$

Note. The point \( x_0 \) is where the function f(x) may converge if it has a finite maximum. $$ M = \lim_{n \rightarrow \infty;} f(x_n) = f(x_0) $$

Since f(x) is continuous, the sequence \( f(x_{nk}) \) converges to \( f(x_0) \):

$$ \lim_{n \rightarrow \infty;} f(x_{nk}) = f(x_0) $$

Hence:

$$ \begin{cases} M = \lim_{n \rightarrow \infty;} f(x_n) = f(x_0) \\ \\ \lim_{k \rightarrow \infty;} f(x_{nk}) = f(x_0) \end{cases} $$

which leads to the following equality:

$$ M = \lim_{n \rightarrow \infty;} f(x_n) = \lim_{k \rightarrow \infty} f(x_{nk}) = f(x_0) $$

This shows that the supremum of the function is indeed a finite maximum:

$$ M = f(x_0) = sup \{ f(x) \: \forall x \in [a,b] \} $$

Thus, the limit of the sequence \( f(x_n) \) converges to a finite value M rather than diverging to infinity:

$$ \lim_{n \rightarrow \infty} f(x_n) = M $$

Note. The same reasoning applies for finding the point of minimum, starting from the infimum m = f(x) over the closed interval [a,b].

Weierstrass’ Theorem for Functions of Two or More Variables

Let \( A \subseteq \mathbb{R}^n \) be a compact set (meaning it’s closed and bounded), and let \( f : A \to \mathbb{R} \) be continuous. Then \( f \) attains both an absolute minimum and an absolute maximum on \( A \). In other words, there exist points \( x_{\text{min}}, x_{\text{max}} \in A \) such that \[f(x_{\text{min}}) \le f(x) \le f(x_{\text{max}}) \quad \forall x \in A.\]

This is the natural generalization of Weierstrass’ theorem to multivariable functions.

Here, we speak of compactness because the domain must be both closed and bounded.

Note. For single-variable functions \( f(x) \), the domain in Weierstrass’ theorem is a closed and bounded interval \( [a,b] \) on the real number line, with two endpoints. For functions of two variables \( f(x,y) \), the domain instead consists of a set of points in the plane \( \mathbb{R}^2 \), such as a closed disk \( x^2+y^2 \le r^2 \). In this context, the “boundaries” of the domain correspond to the perimeter of the set - for example, the circle defining the edge of the disk.

Example

Let’s examine a function of two variables:

\[ f(x,y) = x^2 + y^2 \]

and define the domain as the closed disk of radius 1 centered at the origin (0,0):

\[ A = \{ (x,y) \in \mathbb{R}^2 \mid x^2 + y^2 \leq 1 \} \]

The set \( A \) is closed because it includes its boundary \( x^2 + y^2 = 1 \), and bounded because it lies within a circle of radius 1.

Hence, the set \( A \) is compact.

The function \( f(x,y) = x^2 + y^2 \) is continuous throughout \( \mathbb{R}^2 \) and therefore also continuous over the domain \( A \).

By Weierstrass’ theorem, \( f \) must attain both an absolute maximum and minimum over \( A \).

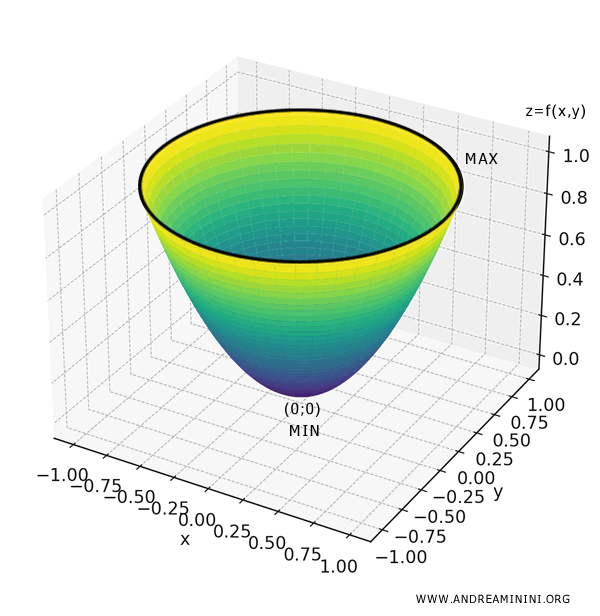
In this case, the absolute minimum occurs at \( x=0 \) and \( y=0 \), the center of the disk, where \( f(0,0) = 0 \).

The absolute maximum occurs along the entire boundary of the disk, where \( x^2 + y^2 = 1 \) and \( f(x,y) = 1 \). Thus, instead of a single point of absolute maximum, there are infinitely many points lying along the circle.

And so on.