Intermediate Value Theorem
A function f(x) that is continuous on a closed interval [a, b] attains every value between f(a) and f(b). This result is also known as the Theorem of All Values.
The theorem applies to real-valued continuous functions.
Specifically, it states that the image [f(a), f(b)] of the interval [a, b] includes every real number between the function’s values at the endpoints f(a) and f(b).
A Practical Example
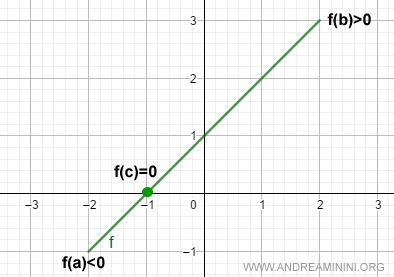
Consider the following continuous function on the interval [-2, 2]:
$$ f(x) = x + 1 $$
This function is negative at the left endpoint a = -2 and positive at the right endpoint b = 2:
$$ f(a) = f(-2) = -1 $$
$$ f(b) = f(2) = 3 $$
Between f(a) and f(b), the function takes on every intermediate value for some x in [a, b].

Proof Explained
Let’s consider a continuous function where f(a) is less than or equal to f(b):
$$ f(a) \le f(b) $$
By the Intermediate Value Theorem:
$$ \forall \; y_0 \in [f(a), f(b)], \; \exists \; x_0 \in [a, b] \; \text{such that} \; f(x_0) = y_0 $$
To establish this, we define a new function g(x) that measures the difference between f(x) and any chosen value y0 in [f(a), f(b)]:
$$ g(x) = f(x) - y_0, \quad \forall \; x \in [a, b] $$
We then evaluate g(x) at the interval’s endpoints:
$$ g(a) = f(a) - y_0 $$
$$ g(b) = f(b) - y_0 $$
Since f(a) < f(b), the chosen value y0 lies strictly between these endpoint values:
$$ f(a) < y_0 < f(b) $$
Thus:
$$ g(a) = f(a) - y_0 < 0 $$
$$ g(b) = f(b) - y_0 > 0 $$
This indicates that g(x) changes sign on the interval [a, b].
By the Zero Existence Theorem, there must exist at least one point x0 in (a, b) where:
$$ g(x_0) = 0 $$
Therefore:
$$ f(x_0) = y_0 $$
Since f(x) is continuous, the existence of x0 guarantees that the function attains every value between f(a) and f(b) for some x in [a, b].
Corollary: Existence of Values Between the Minimum and Maximum
If a function is continuous on a closed interval [a, b], it attains every value between its minimum (m) and maximum (M).
Proof
By the Weierstrass Theorem, any continuous function on [a, b] achieves both a minimum m and a maximum M.
We want to prove that for any value y0 in [m, M], there exists a point x0 in [a, b] such that:
$$ f(x_0) = y_0 $$
Consider the points where the minimum and maximum occur, x1 and x2:
$$ m = f(x_1) $$
$$ M = f(x_2) $$
Define the difference function:
$$ h(x) = f(x) - y_0 $$
Since m < y0, it follows that h(x) is negative at the minimum point x1:
$$ h(x_1) = f(x_1) - y_0 < 0 $$
And because M > y0, h(x) is positive at the maximum point x2:
$$ h(x_2) = f(x_2) - y_0 > 0 $$
By the Zero Existence Theorem, there must be a point x0 in the open interval (x1, x2) such that:
$$ h(x_0) = 0 $$
Therefore:
$$ f(x_0) = y_0 $$
This proves that for every y0 in [m, M], there is at least one x0 in [a, b] such that f(x0) = y0.
Because the function f(x) is continuous on [a, b], the same reasoning holds for all values y0 in (m, M).
Hence, for any y0 in (m, M), there exists a point x0 in the domain such that f(x0) = y0.
This completes the proof of the Intermediate Value Theorem.
And so on.
