Bolzano’s Theorem

According to the Zero Existence Theorem (also known as Bolzano’s Theorem), if a function f(x) is continuous on a closed interval [a, b] and satisfies f(a) < 0 and f(b) > 0, then there exists at least one point x₀ in (a, b) such that f(x₀) = 0 - that is, the function has a root within the interval.

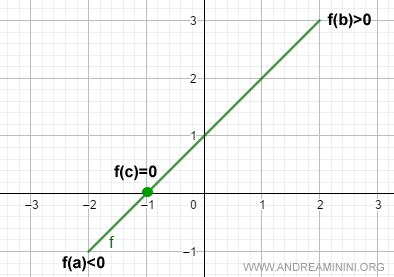
The theorem also applies in the opposite case, where f(a) > 0 and f(b) < 0.

The essential condition for the theorem to hold is that the function takes on opposite signs at the endpoints f(a) and f(b).

A Practical Example

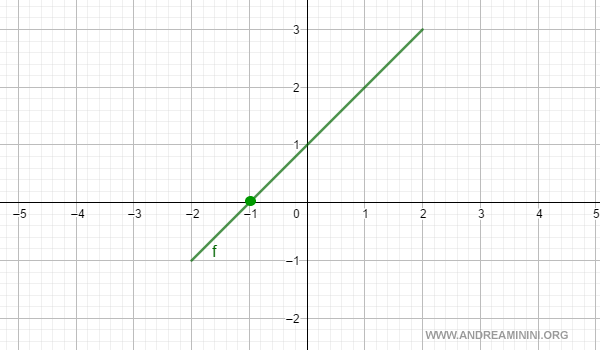
Consider the function:

$$ f(x) = x + 1 $$

over the closed interval [-2, +2].

At the intermediate point x₀ = -1, the function equals zero:

$$ f(-1) = 0 $$

Although simple, this example clearly illustrates the theorem’s significance.

Proof Explained

Let f(x) be a continuous function defined on [a, b].

At the endpoints, the function takes values of opposite sign:

$$ f(a) < 0 $$

$$ f(b) > 0 $$

Consider the midpoint c of the interval [a, b]:

$$ c = \frac{a + b}{2} $$

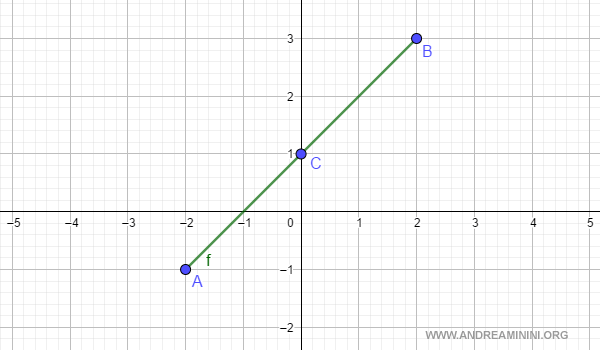
Example. Let’s revisit the previous example. The function f(x) = x + 1 is defined on [-2, 2]. Here, f(a) = f(-2) = -1, while f(b) = f(2) = 3. At the midpoint c = 0, the function takes the value f(c) = f(0) = 1.

We now examine the value of f(x) at the midpoint c:

• If f(c) > 0: $$ f(c) > 0 $$ The function has the opposite sign compared to f(a) < 0. We then consider the subinterval [a, c]: $$ [a_1, b_1] = [a, c] $$ and find its new midpoint: $$ c_2 = \frac{a_1 + c_1}{2} $$ and continue this process iteratively.
• If f(c) < 0: $$ f(c) < 0 $$ The function has the same sign as f(a) < 0. In this case, we focus on the subinterval [c, b]: $$ [a_1, b_1] = [c, b] $$ and determine its midpoint: $$ c_2 = \frac{c_1 + b_1}{2} $$ repeating the procedure as needed.

Example. In the previous example, f(c) = 1, so f(c) > 0. Therefore, we choose the new interval [a₁, b₁] = [a, c]. Next, we find a new midpoint c₁.

We repeat this procedure as many times as necessary until we reach a point where f(c) = 0 - that is, until we locate a root. Once f(c) = 0, the iteration terminates.

Through this iterative method, we generate three sequences:

$$ a_n, \; b_n, \; c_n $$

As long as f(c) ≠ 0, the function maintains opposite signs at the endpoints of the interval:

$$ f(a_n) < 0 $$ $$ f(b_n) > 0 $$

With each iteration, the length of the interval [a_n, b_n] is halved:

$$ b_1 - a_1 = \frac{b - a}{2} $$

$$ b_2 - a_2 = \frac{b - a}{2^2} $$

$$ \vdots $$

Therefore, after n iterations, the length of the interval is:

$$ b_n - a_n = \frac{b - a}{2^n} $$

The sequence a_n is clearly increasing, since:

$$ a_1 \le a_2 \le \dots \le a_n $$

Moreover, the sequence a_n is bounded because it remains confined within the interval [a, b].

Since it is increasing and bounded, by the Monotone Convergence Theorem, the sequence a_n converges to a finite limit, which we denote as x₀:

$$ \lim_{n \rightarrow \infty} a_n = x_0 $$

The sequence b_n can be determined from the interval length:

$$ b_n - a_n = \frac{b - a}{2^n} $$

$$ b_n = a_n + \frac{b - a}{2^n} $$

Since $$ \frac{b - a}{2^n} \rightarrow 0 $$ as n → ∞, it follows that the limit of b_n coincides with that of a_n:

$$ \lim_{n \rightarrow \infty} b_n $$

$$ \lim_{n \rightarrow \infty} \left(a_n + \frac{b - a}{2^n}\right) = x_0 $$

Thus, both sequences a_n and b_n converge to x₀ as n approaches infinity:

$$ \lim_{n \rightarrow \infty} a_n = x_0 $$

$$ \lim_{n \rightarrow \infty} b_n = x_0 $$

Moreover, the sequence a_n approaches x₀ from below, while b_n approaches it from above:

$$ a_n \le x_0 \le b_n $$

The value of the function f(x) at the point x₀ can be approximated by the limits of the function values at a_n and b_n as n → ∞:

$$ f(x_0) = \lim_{n \rightarrow \infty} f(a_n) $$

$$ f(x_0) = \lim_{n \rightarrow \infty} f(b_n) $$

However, the first is an underestimate of f(x₀), while the second is an overestimate:

Given that f(a_n) ≤ 0 and f(b_n) ≥ 0, we have:

$$ f(x_0) = \lim_{n \rightarrow \infty} f(a_n) \le 0 $$

$$ f(x_0) = \lim_{n \rightarrow \infty} f(b_n) \ge 0 $$

Thus, the only possibility is:

$$ f(x_0) = 0 $$

This completes the proof of the Zero Existence Theorem.

And so on.