Theorem on the Limit of a Monotonic Function

If a function f(x) is monotonic over the closed interval [a,b], then it has finite limits at every point \( x_0 \) within (a,b): $$ \lim_{x \rightarrow x_0^-} = l \\ \lim_{x \rightarrow x_0^+} = l $$ as well as a finite right-hand limit at the left endpoint: $$ \lim_{x \rightarrow a^+} = l_a $$ and a finite left-hand limit at the right endpoint: $$ \lim_{x \rightarrow b^-} = l_b $$

By “finite limit,” we mean any real number (i.e. not infinity).

What is a monotonic function? A function is called monotonic if it is either always increasing or always decreasing throughout its domain.

A Practical Example

Consider the function \( f(x)=x^3 \) defined on the interval [-1,1]. This function is strictly increasing and therefore monotonic.

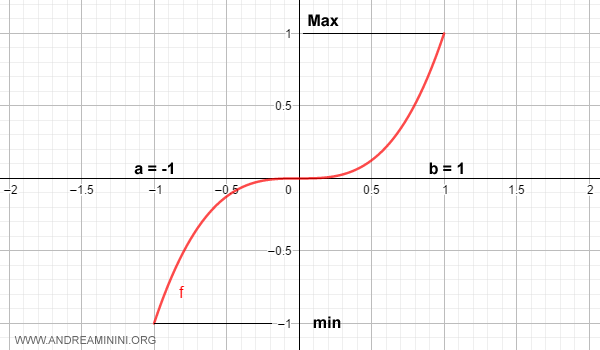
At every point \( x_0 \) in the interval (-1,1), the limit of f(x) as x approaches \( x_0 \) exists and is finite.

Hence, the left-hand and right-hand limits coincide:

$$ \lim_{x \rightarrow x_0^-} x^3 = \lim_{x \rightarrow x_0^+} x^3 = f(x_0) $$

At the left endpoint a = -1, there exists a finite right-hand limit:

$$ \lim_{x \rightarrow a^+} x^3 = f(a) $$

At the right endpoint b = 1, there exists a finite left-hand limit:

$$ \lim_{x \rightarrow b^-} x^3 = f(b) $$

Proof Explained

Let’s analyze a function f(x) that is increasing over the closed interval [a,b].

Since it’s increasing on [a,b], the function attains a minimum value f(a) and a maximum value f(b).

Example. The function \( f(x) = \frac{x}{2} \) is strictly increasing on the closed interval [2,6], where it takes a minimum value of f(2)=1 and a maximum value of f(6)=3.

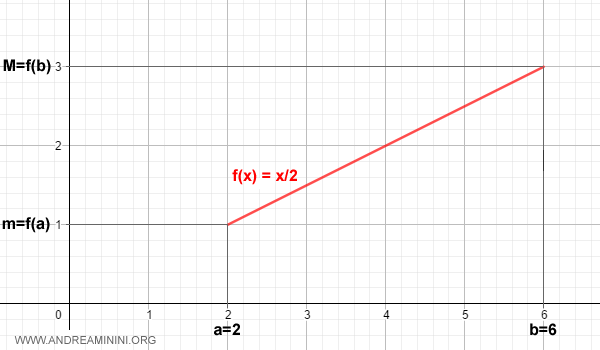
Thus, for any x in [a,b]:

$$ f(a) \le f(x) \le f(b) \quad \forall x \in [a,b] $$

Consider an arbitrary point \( x_0 \) in the interval (a,b], excluding the minimum endpoint a.

Now, examine the supremum of f(x) over the interval [a, \( x_0 \)) - that is, from the left endpoint a (included) up to, but not including, \( x_0 \):

$$ l' = \sup \left\{ f(x) \;:\; x \in [a, x_0) \right\} $$

Since f(x) is monotonic and bounded above by the finite maximum f(b), the supremum \( l' \) must also be finite.

Example

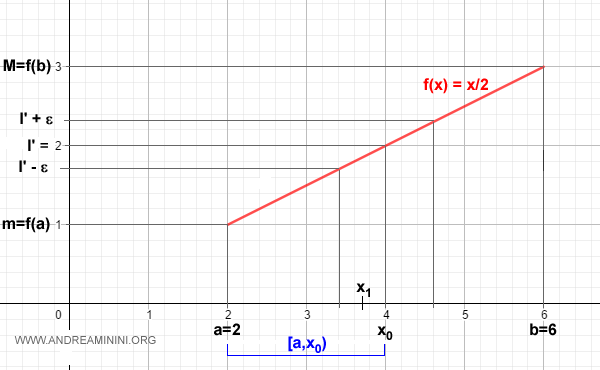
For a continuous monotonic function, given any \( \epsilon > 0 \), there exists a point \( x_1 \) in [a, \( x_0 \)) such that:

$$ l' - \epsilon < f(x_1) $$

Since the supremum \( l' \) exists, we also have:

$$ l' - \epsilon < f(x_1) \le l' < l' + \epsilon $$

Therefore, in an increasing function, for every \( x > x_1 \), we can assert:

$$ l' - \epsilon < f(x_1) \le f(x) \le l' < l' + \epsilon \quad \forall x > x_1 $$

This demonstrates that the finite left-hand limit of f(x) exists as x approaches \( x_0 \):

$$ \lim_{x \rightarrow x_0^-} f(x) = l' $$

Using a similar reasoning, consider a point \( x_0 \) in the interval (\( x_0 \), b].

Now look at the infimum over the interval (\( x_0 \), b]:

$$ l' = \inf \left\{ f(x) \;:\; x \in (x_0, b] \right\} $$

Since f(x) is monotonic and bounded below by the finite minimum f(a), the infimum \( l' \) is likewise finite.

Given any \( \epsilon > 0 \), there exists a point \( x_1 \) in (\( x_0 \), b] such that:

$$ f(x_1) < l' + \epsilon $$

And since the infimum exists:

$$ l' - \epsilon < l' \le f(x_1) < l' + \epsilon $$

Therefore, in an increasing function, for every \( x < x_1 \), we can write:

$$ l' - \epsilon < l' \le f(x) \le f(x_1) < l' + \epsilon \quad \forall x < x_1 $$

This proves that the finite right-hand limit of f(x) exists as x approaches \( x_0 \):

$$ \lim_{x \rightarrow x_0^+} f(x) = l' $$

Since both the left-hand and right-hand limits exist at \( x_0 \), the overall limit of f(x) as x approaches \( x_0 \) is finite:

$$ \lim_{x \rightarrow x_0} f(x) = l' $$

And so on.