Limit from Above and Limit from Below
When a function has a finite limit \( l \) as \( x \to x_0 \), we can describe more precisely how the function approaches that value. In particular, it may approach it from above or from below. This distinction gives rise to the notions of a limit from above and a limit from below.
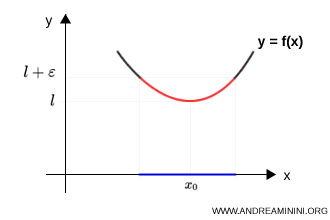
From a practical standpoint, by inspecting the graph of the function, we observe that:
- in the case of a limit from above, the graph of the function approaches the line \( y = l \) from above
- in the case of a limit from below, the graph approaches the same line from below
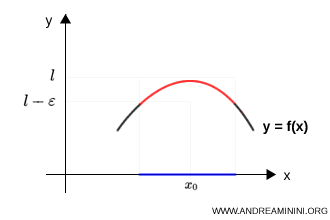
The numerical value of the limit is the same in both cases, but the local behavior of the function differs.
Note. The idea is straightforward: it is not enough to know which number the function approaches, we must also know from which side it approaches it. Limits from above and from below are therefore not new kinds of limits, but rather a qualitative refinement of the concept of a finite limit.
The Limit from Above
We say that a function \( f(x) \) tends to the value \( l \) from above if:
- the limit of \( f(x) \) as \( x \to x_0 \) is \( l \)
- in a neighborhood of \( x_0 \), possibly excluding the point \( x_0 \) itself, the function takes only values greater than \( l \)
Symbolically, this is written as:
\[ \lim_{x \to x_0} f(x) = l^{+} \]
From an analytical perspective, this is equivalent to requiring that for every \( \varepsilon > 0 \), there exists a suitable neighborhood of \( x_0 \) such that:
\[ l < f(x) < l + \varepsilon \]
Subtracting $ l $ from each term of the inequality yields:
\[ 0 < f(x) - l < \varepsilon \]
In other words, the function \( f(x) \) approaches \( l \) while remaining strictly above that value.

For example, if a function has limit \( l = 2 \) and, as \( x \) approaches \( x_0 \), takes values such as 2.1, 2.01, 2.001, ... without ever reaching or dropping below 2, then the function approaches 2 from above and the limit is from above.
Example
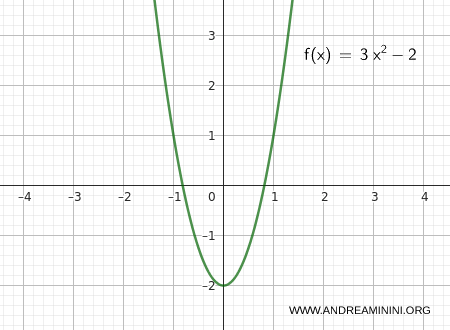
Consider the function:
\[ f(x) = 3x^2 - 2 \]
We want to verify that:
\[ \lim_{x \to 0} (3x^2 - 2) = -2^{+} \]
Fix a number \( \varepsilon > 0 \) and impose the condition:
\[ 0 < f(x) - l < \varepsilon \]
Since $ f(x) = 3x^2 - 2 $ and $ l = -2 $:
\[ 0 < (3x^2 - 2) - (-2) < \varepsilon \]
\[ 0 < 3x^2 < \varepsilon \]
The first inequality \( 0 < 3x^2 \) holds for all \( x \neq 0 \), since \( x^2 > 0 \).
The second inequality \( 3x^2 < \varepsilon \) allows us to solve for the variable x:
\[ x^2 < \frac{\varepsilon}{3} \]
that is,
\[ -\frac{\sqrt{\varepsilon}}{3} < x < \frac{\sqrt{\varepsilon}}{3} \]
Within this neighborhood of \( 0 \), excluding the point \( x = 0 \), the following condition is satisfied:
\[ -2 < f(x) < -2 + \varepsilon \]
Therefore, the function approaches -2 from above and the limit is from above.
The Limit from Below
We say that a function \( f(x) \) tends to the value \( l \) from below if:
- the limit of \( f(x) \) as \( x \to x_0 \) is \( l \)
- in a neighborhood of \( x_0 \), possibly excluding the point \( x_0 \), the function takes only values less than \( l \)
Symbolically:
\[ \lim_{x \to x_0} f(x) = l^{-} \]
From an analytical point of view, this condition can be written as:
\[ l - \varepsilon < f(x) < l \]
Subtracting $ l $ from each term of the inequality gives:
\[ - \varepsilon < f(x) - l < 0 \]
In this case, the function \( f(x) \) approaches \( l \) while remaining strictly below that value.

For instance, if a function has limit \( l = 2 \) and, as it approaches \( x_0 \), takes values such as 1.9, 1.99, 1.999, ... without ever exceeding 2, then the limit is from below.
Example
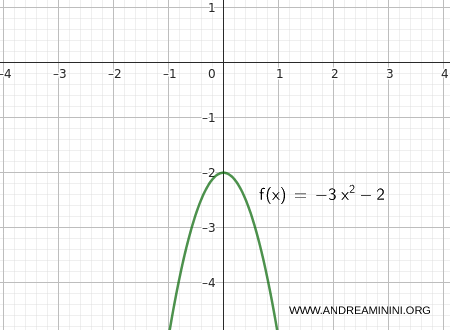
Consider the function:
\[ f(x) = -3x^2 - 2 \]
We want to verify that:
\[ \lim_{x \to 0} (-3x^2 - 2) = -2^{-} \]
Fix a number \( \varepsilon > 0 \) and impose the condition:
\[ -\varepsilon < f(x) - l < 0 \]
\[ -\varepsilon < (-3x^2 - 2) - (-2) < 0 \]
\[ -\varepsilon < -3x^2 < 0 \]
The second inequality \( -3x^2 < 0 \) is always satisfied for \( x \neq 0 \), since \( x^2 > 0 \) and the coefficient \( -3 < 0 \). The product of a positive number and a negative number is therefore negative, that is, less than zero.
The first inequality \( -\varepsilon < -3x^2 \) allows us to solve for the variable x:
Divide both sides of the inequality by -3. When an inequality is divided by a negative number, its direction is reversed.
\( \frac{-\varepsilon}{-3} > \frac{-3x^2}{-3} \]
\( \frac{\varepsilon}{3} > x^2 \]
that is,
\[ - \sqrt{ \frac{\varepsilon}{3} } < x < \sqrt{ \frac{\varepsilon}{3} } \]
Within this neighborhood of \( 0 \), excluding the point \( x = 0 \), the following condition holds:
\[ -2 - \varepsilon < f(x) < -2 \]
Therefore, the function \( f(x) \) approaches -2 from below and the limit is from below.
And so on.
