Indeterminate Forms in Limits

When working with limits, you may come across an indeterminate form - a situation where the result isn’t immediately clear and further analysis is required. These are the most common indeterminate forms in limit problems:

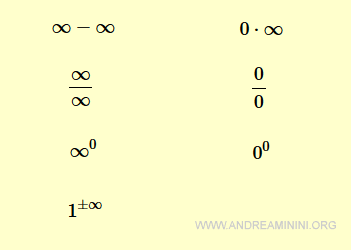
Just because a limit results in an indeterminate form doesn’t mean the limit doesn’t exist.

To evaluate it, the expression must be rewritten or simplified in a way that removes the source of indeterminacy.

How to Resolve an Indeterminate Form

There are several strategies you can use to evaluate limits that take on an indeterminate form:

• Algebraic manipulation. Sometimes, a limit becomes solvable after applying a few algebraic transformations. Rewriting the expression in an equivalent form can often eliminate the ambiguity. However, this approach isn’t always straightforward, and a suitable transformation may not always exist.

  Example 1. This limit presents an indeterminate form of type 0/0: $$ \lim_{n \rightarrow \infty} \ \frac{\frac{1}{n^2}}{\frac{1}{n}} = \frac{0}{0} $$ By simplifying the expression algebraically, we can resolve the indeterminacy: $$ \lim_{n \rightarrow \infty} \frac{1}{n^2} \cdot \frac{n}{1} = \lim_{n \rightarrow \infty} \frac{1}{n} = 0 $$ 
  

• Special limits. Some limits that produce indeterminate forms can be evaluated by applying the special limits studied in mathematical analysis. In these cases, the expression of the limit is algebraically transformed until it can be reduced to one of the well known fundamental limits.
• Taylor series expansions. Some limits can be evaluated by replacing exponential, logarithmic, or trigonometric functions with their Taylor series expansions, approximating the functions with polynomials that describe their local behavior.
• L'Hôpital's rule. If the function is differentiable and the indeterminate form is \(0/0\) or \(\infty/\infty\), L'Hôpital's rule can be applied by studying the limit of the derivatives of the numerator and the denominator. The procedure may be repeated by taking the first, second, third derivative, and so on, until the limit becomes determined, either finite or infinite. In practice, L'Hôpital's rule is frequently used when logarithmic, exponential, or trigonometric functions appear.
  

  Example. This limit has the indeterminate form \(\infty/\infty\) $$ \lim_{x \rightarrow \infty} \frac{e^x}{x} = \frac{\infty}{\infty} $$ Apply L'Hôpital's rule and compute the derivatives of the numerator and the denominator $$ \lim_{x \rightarrow \infty} \frac{D[e^x]}{D[x]} = \lim_{x \rightarrow \infty} \frac{e^x}{1} = + \infty $$ Therefore, the limit diverges.

Using the Conjugate

In some limits we encounter a difference between two terms that contain a square root. This situation often leads to an indeterminate form of the type \(+\infty - \infty \).

In these cases it is often useful to multiply the expression by the conjugate.

The idea is to multiply and divide the expression by the conjugate of the difference, that is, the same expression with the opposite sign between the terms. This allows us to apply the algebraic identity \( (a-b)(a+b)=a^2-b^2 \), which removes the square root and simplifies the expression.

Example

Consider the following limit as $ x \to \infty $, where the expression contains a difference between two terms involving a square root

\[ \lim_{x \to \infty} x-\sqrt{x^2+1} \]

This expression produces an indeterminate form of the type \(+\infty - \infty \).

\[ \lim_{x \to \infty} x-\sqrt{x^2+1} = +\infty - \infty  \]

To evaluate the limit, multiply and divide by the conjugate of \( x-\sqrt{x^2+1} \), namely \( x + \sqrt{x^2+1} \).

\[ x-\sqrt{x^2+1} =  x-\sqrt{x^2+1} \cdot \frac{ x + \sqrt{x^2+1} }{ x + \sqrt{x^2+1}  } \]

The expression \(  ( x-\sqrt{x^2+1} ) \cdot ( x + \sqrt{x^2+1} ) \) is a difference of squares \( x^2 - ( \sqrt{x^2+1} )^2 \). Therefore we can rewrite the expression in an equivalent form:

\[ \frac{ x^2 - ( \sqrt{x^2+1} )^2 }{ x + \sqrt{x^2+1}  } \]

At this point the square root disappears from the numerator

\[  \frac{ x^2 - ( x^2+1) }{ x + \sqrt{x^2+1}  } \]

\[ \frac{ -1 }{ x + \sqrt{x^2+1}  } \]

The expression is now much easier to analyze.

As $ x \to \infty $, the denominator grows without bound, so the limit of the equivalent function tends to zero.

\[ \lim_{x \to \infty} \frac{ -1 }{ x + \sqrt{x^2+1}  }  = 0 \]

Therefore, the original limit as $ x \to \infty $ also tends to zero

\[ \lim_{x \to \infty} x-\sqrt{x^2+1} =  \lim_{x \to \infty} \frac{ -1 }{ x + \sqrt{x^2+1}  }  = 0 \]

This example shows that multiplying by the conjugate is a useful algebraic technique for evaluating limits that involve a difference between expressions containing square roots.

Factoring out the highest power of \(x\)

When evaluating the limit of a polynomial function as \( x \to +\infty \) or \( x \to -\infty \), the expression may take the indeterminate form \( \infty - \infty \).

\[ \lim_{x \to +\infty \atop (x \to -\infty)} \left( a_0 x^n + a_1 x^{n-1} + \dots + a_n \right) = \infty - \infty \]

This indeterminate form can be resolved by factoring out the highest power of \( x \) that appears in the polynomial.

\[ \lim_{x \to +\infty \atop (x \to -\infty)} x^n \left( a_0 + \frac{a_1}{x} + \frac{a_2}{x^2} + \dots + \frac{a_n}{x^n} \right) \]

In this way, the polynomial is rewritten as the product of \( x^n \) and a factor containing terms such as \( \frac{a_1}{x}, \frac{a_2}{x^2}, \dots \).

Since the terms \( \frac{a_1}{x}, \frac{a_2}{x^2}, \dots \) tend to \( 0 \) as \( x \to \pm \infty \), the expression inside the parentheses approaches the coefficient of the highest-degree term.

The behavior of the limit is therefore determined by the dominant term \( a_0 x^n \), which establishes whether the limit diverges to \( +\infty \) or to \( -\infty \).

\[ \lim_{x \to +\infty \atop (x \to -\infty)} \left( a_0 x^n + a_1 x^{n-1} + \dots + a_n \right) = \lim_{x \to +\infty \atop (x \to -\infty)} a_0 x^n \]

The sign of the limit follows from the usual sign rules applied to the product \( a_0 x^n \).

Example

Consider the limit

\[ \lim_{x \to +\infty} (3x^2 - 5x + 1) \]

To remove the indeterminate form, factor out the highest power of \( x \), which is \( x^2 \):

\[ 3x^2 - 5x + 1 = x^2 \left(3 - \frac{5}{x} + \frac{1}{x^2}\right) \]

The limit then becomes

\[ \lim_{x \to +\infty} x^2 \left(3 - \frac{5}{x} + \frac{1}{x^2}\right) \]

As \( x \to \infty \), the terms \( \frac{5}{x} \) and \( \frac{1}{x^2} \) approach zero. The expression inside the parentheses therefore approaches \( 3 \), and the behavior of the limit is governed by the dominant term \( 3x^2 \).

\[ \lim_{x \to +\infty} x^2 \left(3 - \frac{5}{x} + \frac{1}{x^2}\right) = \lim_{x \to +\infty} 3x^2 = +\infty \]

Therefore, the original limit also diverges

\[ \lim_{x \to +\infty} (3x^2 - 5x + 1) = +\infty \]

This technique allows us to resolve indeterminate forms \(  \infty - \infty \) that arise in limits of polynomial functions as \( x \to \pm \infty \).

Note. In limits of polynomial functions as \( x \to \pm\infty \), it is often sufficient to consider only the highest-degree term without carrying out all intermediate steps. A polynomial is asymptotically equivalent to its dominant term \( a_0 x^n \), while the lower-degree terms become negligible as \( x \to \pm\infty \). Consequently, the behavior of the limit coincides with that of \( a_0 x^n \). For example, the previous exercise could have been solved more quickly in this way \[ \lim_{x \to +\infty} (3x^2 - 5x + 1) = \lim_{x \to +\infty} 3x^2 = +\infty \]

Limits Involving the Indeterminate Form \( 0 \cdot \infty \)

The indeterminate form \( 0 \cdot \infty \) arises when, in a limit, one factor approaches zero while the other tends to infinity.

\[ \lim_{x \to a} f(x) g(x) = 0 \cdot \infty \]

In this situation the value of the limit cannot be determined immediately, because the result depends on how rapidly the two factors approach \( 0 \) and \( \infty \), respectively.

To evaluate this type of limit, the product is usually rewritten as a quotient.

\[ f(x) g(x) = \frac{f(x)}{\frac{1}{g(x)}} \]

or

\[ f(x) g(x) = \frac{g(x)}{\frac{1}{f(x)}} \]

After this transformation, the limit often becomes one of the simpler indeterminate forms \( \frac{0}{0} \) or \( \frac{\infty}{\infty} \), which can then be studied using standard techniques.

Example

Consider the limit

\[ \lim_{x \to +\infty} x  e^{-x} \]

This is an indeterminate form of type \( 0 \cdot \infty \) because  \(  x \to \infty \) while  \( e^{-x} \to 0 \).

\[ \lim_{x \to +\infty} x  e^{-x} = 0 \cdot \infty \]

Rewrite the product as a quotient

\[ x e^{-x} = \frac{x}{e^{x}} \]

The limit becomes

\[ \lim_{x \to +\infty} \frac{x}{e^{x}} = \frac{\infty}{\infty} \]

Since the exponential function grows faster than any polynomial, the limit is

\[ \lim_{x \to +\infty} \frac{x}{e^{x}} = 0 \]

Therefore, when the form \( 0 \cdot \infty \) appears, the key step is to rewrite the product as a quotient.

This transformation converts the limit into a simpler indeterminate form that can be analyzed using standard methods.

Limits with the indeterminate form \( \frac{\infty}{\infty} \)

When a limit takes the indeterminate form \( \frac{\infty}{\infty} \), both the numerator and the denominator diverge as the variable approaches a given value, most commonly \( x \to \infty \) or \( x \to -\infty \).

In this situation, the limit cannot be evaluated by direct substitution. The expression must first be rewritten or simplified.

Three techniques are commonly used.

1] Factoring out the highest power

This is the simplest method when the limit involves polynomials. The highest power of the variable is factored out from both the numerator and the denominator.

Example

\[ \lim_{x \to \infty} \frac{3x^2 - 5x + 1}{2x^2 + x} \]

Factor out the highest power \( x^2 \)

\[ \frac{x^2(3 - \frac{5}{x} + \frac{1}{x^2})}{x^2(2 + \frac{1}{x})} \]

Then simplify \( x^2 \)

\[ \frac{3 - \frac{5}{x} + \frac{1}{x^2}}{2 + \frac{1}{x}} \]

As \( x \to \infty \), the terms \( \frac{5}{x} \) and \( \frac{1}{x^2} \) tend to zero.

\[ \lim_{x \to \infty} \frac{3x^2 - 5x + 1}{2x^2 + x} = \frac{3}{2} \]

In practice, the behavior of the limit is determined by the terms of highest degree.

Note. When a limit involves only polynomials, it is usually unnecessary to carry out all the intermediate steps. The value of the limit depends solely on the ratio of the leading terms. In other words, it is sufficient to compare the degrees of the two polynomials. \[  \lim_{x \to \pm \infty}
\frac{a_0 x^n + a_1 x^{n-1} + \dots + a_n} {b_0 x^m + b_1 x^{m-1} + \dots + b_m} = \begin{cases} \pm \infty & \text{if } n > m  \\ \\ \dfrac{a_0}{b_0} & \text{if } n = m   \\ \\ 0 & \text{if } n < m \end{cases} \] For example, consider the limit \[ \lim_{x \to \infty} \frac{5x^4 + x}{2x^4 - 3x^2} \] The behavior of the function is determined by the ratio of the leading terms \(  \frac{5x^4}{2x^4} \), so the limit approaches \( \frac{5}{2} \) \[ \lim_{x \to \infty} \frac{5x^4 + x}{2x^4 - 3x^2} = \frac{5}{2} \]

2] Dividing by the highest power

This method relies on the same idea as the previous one, but it is written explicitly as a division.

For example, consider the following limit

\[ \lim_{x \to \infty} \frac{4x^3 + x}{2x^3 - 5} \]

Divide every term in the numerator and the denominator by the highest power \( x^3 \)

\[  \lim_{x \to \infty} \frac{4 + \frac{1}{x^2}}{2 - \frac{5}{x^3}} \]

As \( x \to \infty \), the terms \( \frac{1}{x^2} \) and \( \frac{5}{x^3} \) tend to zero.

Therefore, the limit approaches two.

\[  \lim_{x \to \infty} \frac{4 + \frac{1}{x^2}}{2 - \frac{5}{x^3}} = \frac{4}{2} = 2 \]

3] L'Hôpital's rule

If the limit involves more complex functions, such as logarithms, exponentials, or trigonometric functions, we can apply L'Hôpital's rule.

For example, consider the limit

\[ \lim_{x \to \infty} \frac{\ln x}{x} = \frac{\infty}{\infty} \]

Differentiate the numerator and the denominator

\[ \lim_{x \to \infty} \frac{ D[\ln x] }{ D[x] } \]

Since \( D[\ln x] = \frac{1}{x} \) and \( D[x] = 1 \), substitute these results

\[ \lim_{x \to \infty} \frac{ \frac{1}{x} }{ 1 } \]

\[ \lim_{x \to \infty} \frac{1}{x} = 0 \]

Therefore, the limit of the original function as \( x \to \infty \) is also zero.

\[ \lim_{x \to \infty} \frac{\ln x}{x} = 0 \]

Note. In addition to the three methods described above, other techniques may be used depending on the form of the expression when dealing with limits of the indeterminate form \( \frac{\infty}{\infty} \). For instance, one can apply special limits when trigonometric, logarithmic, or exponential functions appear in the expression. In other situations, it may be useful to perform algebraic transformations, such as factorization, extracting common factors, or rationalization. Sometimes the expression can also be simplified by identifying the dominant terms of the function. The most appropriate method therefore depends on the structure of the expression and on the types of functions involved in the limit.

Determinate Forms

Not every occurrence of zero or infinity in a limit leads to an indeterminate form.

For example, the following expressions are not indeterminate:

$$ k + \infty = +\infty $$	A real number k added to infinity
$$ k - \infty = -\infty $$	A real number k minus infinity
$$ \infty+\infty = \infty $$	Infinity plus infinity
$$ k \cdot \infty = \infty $$	A nonzero constant k multiplied by infinity
$$ \infty \cdot \infty = \infty $$	Infinity times infinity
$$ \frac{k}{\infty} = 0 $$	A constant k divided by infinity
$$ \frac{0}{\infty} = 0 $$	Zero divided by infinity
$$ \frac{\infty}{k} = \infty $$	Infinity divided by a nonzero constant k
$$ \frac{k}{0} = \infty $$	A nonzero constant k divided by zero

In these cases, the outcome is algebraically clear and well-defined. They are not considered indeterminate forms.

And so on.