Continuity Criterion for Monotonic Functions

A function f(x) that is monotonic over a closed and bounded interval [a,b] is also a continuous function if and only if its image Im(f) includes every value between the endpoints f(a) and f(b). $$ Im(f) = \{ f(a), ... , f(b) \} $$

A Practical Example

Consider the function f(x), which is strictly increasing on the interval [-1,1]:

$$ f(x) = x^3 \:\:\: \forall x \in [-1,1] $$

Here’s its graph:

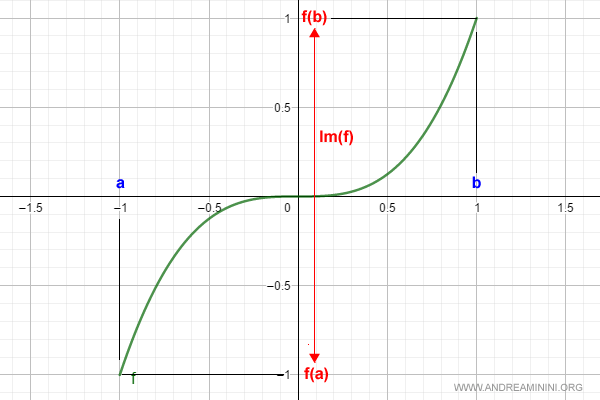
The image of the function f(x) covers every value between f(a) and f(b).

Therefore, f(x) is continuous on the interval [-1,1].

Proof Explained

A function f(x) is monotonic if it is either increasing or decreasing throughout the closed interval [a,b].

When the Function is Continuous

If the function is continuous, then all its values lie between f(a) and f(b):

• If the function is increasing: $$ f(a) \le f(x) \le f(b) \:\:\: \forall x \in [a,b] $$
• If the function is decreasing: $$ f(b) \le f(x) \le f(a) \:\:\: \forall x \in [a,b] $$

In both cases, by the Intermediate Value Theorem, the function attains every intermediate value between f(a) and f(b).

This establishes the continuity criterion for monotonic functions.

When the Function is Not Continuous

If f(x) is not continuous at some point \( x_0 \) within the interval (a,b), there is a discontinuity of the first kind at \( x_0 \).

$$ \lim_{x \rightarrow x_0^-} = l_1 < l_2 = \lim_{x \rightarrow x_0^+} $$

In the interval \( (l_1, l_2) \), the function f(x) takes no values.

Consequently, the image of f(x) does not include all values between f(a) and f(b).

This completes the proof of the theorem.

Note. To demonstrate discontinuity at the endpoints, it suffices to consider \( x_0 = a \) or \( x_0 = b \). In either case - regardless of whether the function is increasing or decreasing - the image of f(x) fails to cover all values between f(a) and f(b).

And so on.