Bijective Functions

What Is a Bijective Function?

A function $f(x)$ is said to be bijective (or a one-to-one correspondence) if it is both injective and surjective.

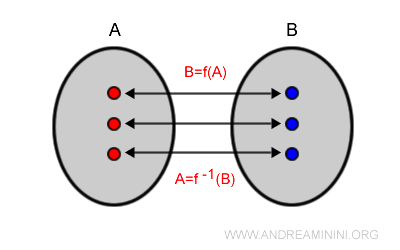
In other words, every element in the domain is paired with exactly one element in the codomain, and every element in the codomain is the image of exactly one element from the domain.

$$ f: A \leftrightarrow B $$

This means:

• Each $x \in A$ maps to a unique $y \in B$
• Each $y \in B$ is mapped from a unique $x \in A$

Note. In a bijective function, each element of the domain has a unique image in the codomain, and each element of the codomain has a unique preimage in the domain. There is a perfect one-to-one matching between the elements of $A$ and $B$.

Bijective functions are also referred to as bijections or one-to-one correspondences.

A Practical Example

The function below is bijective because it satisfies both injectivity and surjectivity:

$$ f(x) = x + 1 $$

Every input $x$ is mapped to a distinct output $y$, and every output $y$ arises from exactly one input $x$.

Thus, the domain and codomain are in a one-to-one correspondence.

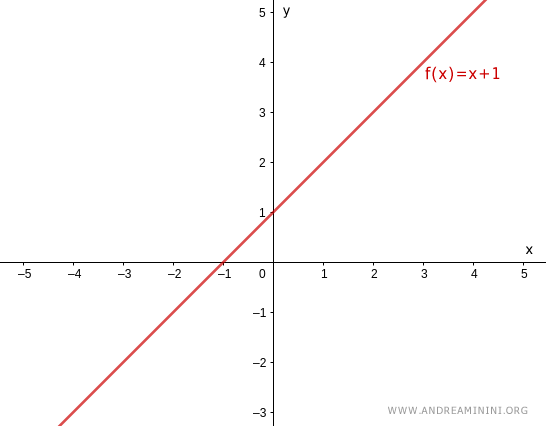
Key Properties of Bijective Functions

Bijective functions have several important characteristics:

• Inverse Function
  Every bijective function is invertible; that is, it has an inverse function: $$ x = f^{-1}(y) $$
• Identity Mapping
  The composition of a bijective function with its inverse yields the identity function: $$ x = f^{-1}(f(x)) $$

  Note. A function is called the identity if it satisfies $f(x) = x$ for all $x$ in its domain.

Example

Consider the function:

$$ y = f(x) = x + 1 $$

This function is bijective and therefore invertible. Its inverse is:

$$ x = f^{-1}(y) = y - 1 $$

Composing the function with its inverse confirms the identity property:

$$ x = f^{-1}(f(x)) $$

Since $f(x) = x + 1$, we compute:

$$ x = f^{-1}(x + 1) $$

Given that $f^{-1}(y) = y - 1$, this becomes:

$$ x = (x + 1) - 1 $$

$$ x = x $$

As expected, the composition returns the original input.