Piecewise Functions

Piecewise functions are defined by different expressions, each applying to a specific range of values for the independent variable.

A practical example

One of the simplest examples of a piecewise function is the absolute value function.

$$ y = |x| $$

This function is defined by two distinct expressions.

The first expression, $x$, applies when $x$ is non-negative, while the second expression, $-x$, applies when $x$ is negative.

$$ y = |x| = \begin{cases} x \ \ \ \ \text{if} \ x \ge 0 \\ \\ -x \ \ \ \ \text{if} \ x \lt 0 \end{cases} $$

The graph of the function is shown below:

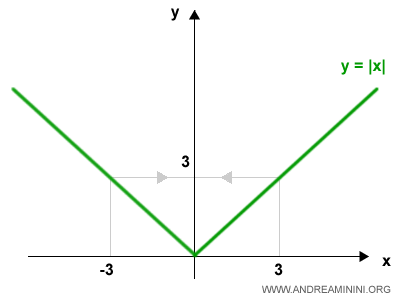
For all non-negative values of $x$, the function increases.

For all negative values of $x$, the function decreases.

And so on.