Domain of a Function

The domain of a function is the set $ A $ of values of the independent variable for which the function is defined. $$ f:A \rightarrow B $$ The set $ A $ represents the collection of admissible inputs of the function. The set $ B $ is the target set and is called the codomain.

In other words, the domain consists of all values for which the algebraic expression of the function is mathematically meaningful.

This set is commonly referred to as the natural domain or the domain of existence of the function.

In most contexts, when one simply refers to the domain, one is implicitly referring to the natural domain, namely the set that follows directly from the analytic form of the function, without introducing any additional restrictions.

The difference between domain and set of definition. In this presentation, the domain and the set of definition coincide and both denote the set of values for which the function is defined. In some textbooks, however, a distinction is made between these two notions: the domain is understood as a set fixed a priori, while the set of definition is the subset of that domain consisting only of the values for which the functional expression is actually meaningful. This distinction is mentioned here solely for the sake of completeness.

In school mathematics, one usually studies functions whose domain is a subset of the real numbers, although functions defined on other numerical sets also exist, such as the complex numbers.

A practical example

Consider two finite sets X and Y.

$$ X = \{1,2,3,4,5 \} $$

$$ Y = \{1,2,3,4,5,6,7,8,9 \} $$

and the relation defined by the rule

$$ f: y = x^2 $$

Not all elements of $ X $ are mapped to an element of $ Y $. For example, $ 4^2 = 16 \not \in Y $.

Therefore, the function is defined only for $ f(1)=1 $, $ f(2)=4 $, $ f(3)=9 $:

$$ D_f = \{1,2,3 \} \subseteq X $$

The set $ D_f $ is called the set of definition (or domain) of the function.

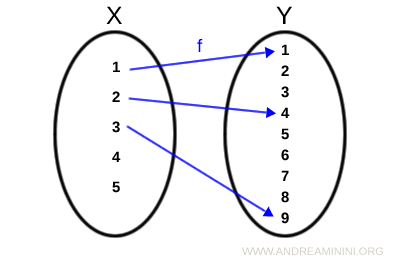
Accordingly, the function can be written as $ f:D_f \rightarrow Y $, with $ f(1)=1 $, $ f(2)=4 $, and $ f(3)=9 $.

Note. As stated above, in this presentation no distinction is made between the domain and the set of definition, which are treated as synonymous. Consequently, $ D_f $ represents both the domain and the set of definition of the function. In textbooks where a distinction is introduced, the set $ X $ is regarded as the domain of the function, fixed a priori, while the set $ D_f = \{1,2,3 \} $ represents the set of definition, that is, the set of values for which the function is actually meaningful. The choice ultimately depends on the adopted notation.

Example 2

Consider the real-valued function

$$ f: y = \sin(x) $$

In this case, both the domain and the codomain coincide with the set of real numbers.

$$ f: R \rightarrow R $$

Here as well, the domain, or set of definition, consists of all values for which the function is well defined.

And so on.