Inverse Proportional Functions

A function is called inversely proportional if it can be expressed as $$ y = \frac{k}{x} $$ where k is a non-zero real constant (k≠0).

The variables x and y are inversely proportional because their product remains constant.

$$ y = \frac{k}{x} $$

Multiplying both sides of the equation by x gives:

$$ y \cdot x = \frac{k}{x} \cdot x $$

which simplifies to a constant product:

$$ y \cdot x = k $$

In other words, if one variable doubles, the other must be halved to keep the product xy unchanged.

This property holds for all values of x except zero, since the function is undefined at x=0 (division by zero).

$$ y = \frac{k}{x} $$

Note. The graph of an inverse proportional function is a rectangular hyperbola. At every point on the curve, the rectangle formed by its projections onto the axes has the same area.

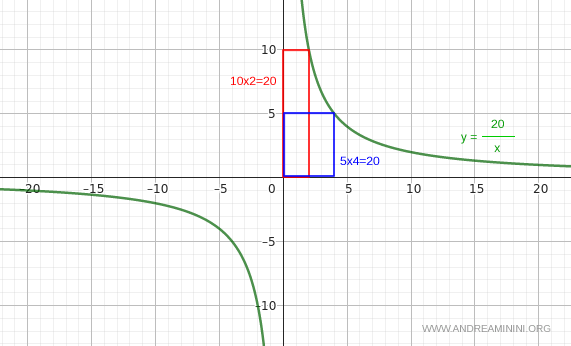
A Worked Example

Consider the function:

$$ y = \frac{20}{x} $$

We want to check whether it satisfies inverse proportionality.

Constructing a table of values for x, y, and their product gives:

$$ \begin{array}{c|c} x & y & x \cdot y \\ \hline -2 & -10 & 20 \\ -1 & -20 & 20 \\ 0 & \text{undef} & \text{undef} \\ 1 & 20 & 20 \\ 2 & 10 & 20 \\ 4 & 5 & 20 \end{array} $$

The product remains constant for every pair (x,y) with x≠0.

Thus, the function y=20/x is indeed an inverse proportional function.

And so on...