Directly Proportional Function

A directly proportional function can be written as $$ y = k \cdot x $$ where k is a non-zero real constant (k≠0).

The variables x and y are said to be directly proportional.

Such functions share the following properties:

• The ratio between the variables, k=y/x, remains constant for every value of x (except when x=0). $$ k = \frac{y}{x} $$
• If one variable is zero (x=0), then the other is also zero (y=0).

Note. This implies that every directly proportional function passes through the origin (0,0). When x is zero, y must also be zero. As a result, the graph of a directly proportional function always goes through the origin O. Here’s a simple example:

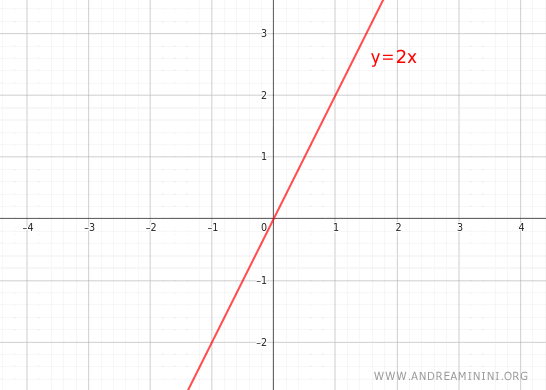
A Practical Example

Consider the function:

$$ y = 2x $$

We can build the following value table:

$$ \begin{array}{c|c} x & y & y/x \\ \hline -1 & -2 & 2 \\ 0 & 0 & - \\ 1 & 2 & 2 \\ 2 & 4 & 2 \\ 3 & 6 & 2 \end{array} $$

Now let’s check whether the function satisfies the conditions for direct proportionality:

• For any non-zero value of x (x≠0), the ratio y/x is always constant and equal to 2.
• The graph of the function passes through the origin (0,0).

Both conditions are met.

Therefore, the function y=2x is a directly proportional function.

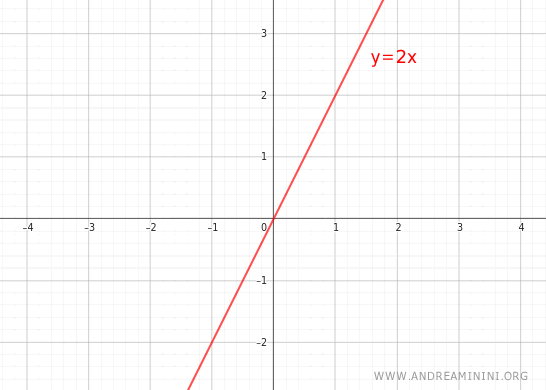
Note. In this case the ratio is 1:2, since the variable y increases at twice the rate of x.

Example 2

Now consider the function:

$$ y=2x-1 $$

The corresponding value table is:

$$ \begin{array}{c|c} x & y & y/x \\ \hline -1 & -3 & 3 \\ 0 & \color{red}{-1} & - \\ 1 & 1 & 1 \\ 2 & 3 & 1.5 \\ 3 & 5 & 1.66 \end{array} $$

In this case, although the graph is a straight line, the function is not directly proportional because it does not pass through the origin (0,0).

Furthermore, the ratio k=y/x is not constant.

And so on...