Horizontal and vertical scaling of a function

A scaling is a geometric transformation that changes the graph of a function in the Cartesian plane by rescaling distances along one axis, while preserving the symmetry of the graph and leaving the origin fixed.

The transformation acts on one of the two coordinate axes: horizontal (x) or vertical (y).

Depending on the value of the scaling factor, the graph either expands or contracts.

Horizontal scaling

Horizontal scaling occurs when the independent variable $x$ is modified inside the function.

$$ y = f\left( \dfrac{x}{m} \right) \quad \text{with } m > 1 $$

The graph expands horizontally with respect to the origin $O$. Each point of the graph is mapped to a position farther from the origin along the $x$ axis.

Example

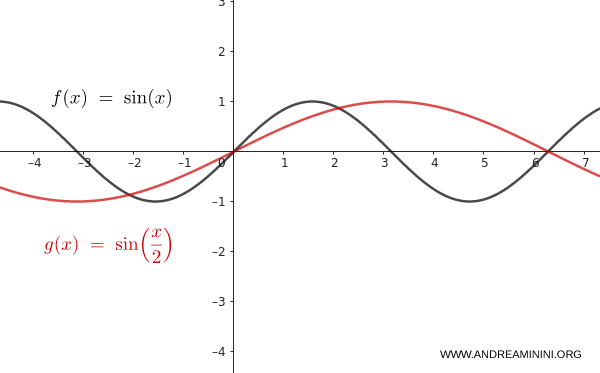
Consider the function $f(x) = \sin(x)$.

Apply a horizontal scaling with $m = 2$:

$$ y = \sin\left( \dfrac{x}{2} \right) $$

The period doubles. The sine wave now requires twice the horizontal distance to complete a full cycle. This corresponds to a horizontal stretch.

Horizontal compression

A horizontal compression occurs when the scaling factor satisfies $0 < m < 1$.

$$ y = f\left( \dfrac{x}{m} \right) \quad \text{with } 0 < m < 1 $$

All points of the graph move closer to the $y$ axis, resulting in a contraction along the horizontal direction.

Example

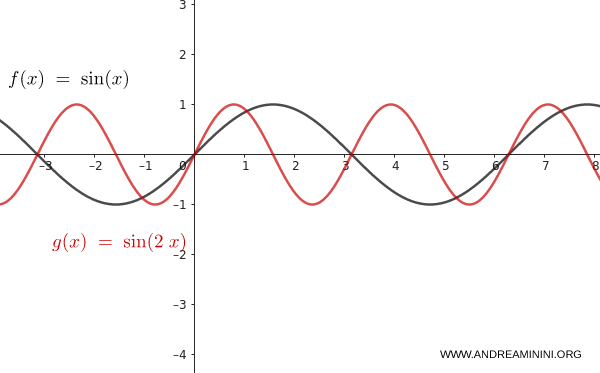
Again, consider the function $f(x) = \sin(x)$.

Apply a horizontal compression with $m = \frac{1}{2}$:

$$ y = \sin(2x) $$

The period is halved. The function completes two full cycles over the same interval in which the original function completes one. This is a horizontal compression.

Vertical scaling

Vertical scaling affects the entire function by multiplying it by a constant factor $n$:

$$ y = n \cdot f(x) \quad \text{with } n > 1 $$

The graph extends upward and downward relative to the $x$ axis. All $y$ values increase in absolute value.

Example

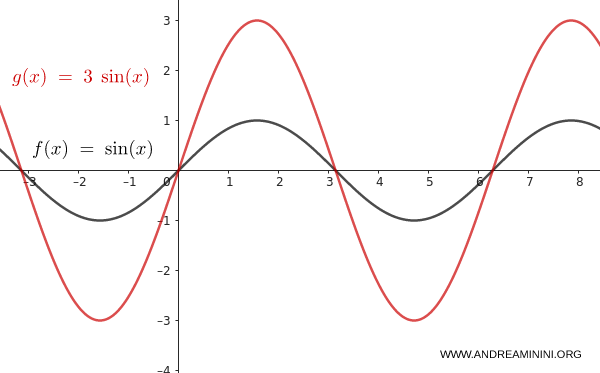
Take the function $f(x) = \sin(x)$.

Apply a vertical scaling with $n = 3$:

$$ y = 3 \cdot \sin(x) $$

The amplitude of the wave triples, increasing from 1 to 3. The shape of the graph is preserved, but it is scaled vertically.

Vertical compression

A vertical compression occurs when the scaling factor satisfies $0 < n < 1$:

$$ y = n \cdot f(x) \quad \text{with } 0 < n < 1 $$

In this case, the amplitude of the graph of the function decreases.

Example

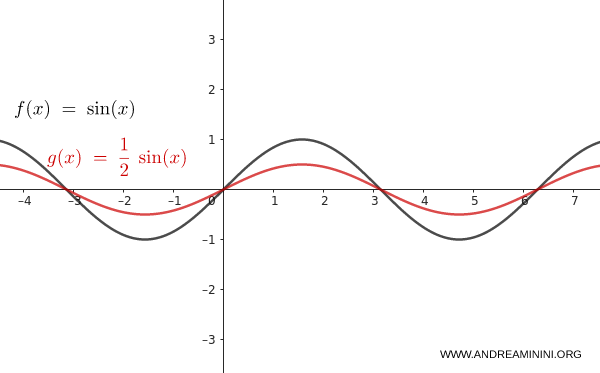
Take $f(x) = \sin(x)$.

Apply a vertical compression with $n = \frac{1}{2}$:

$$ y = \dfrac{1}{2} \cdot \sin(x) $$

The amplitude is reduced from 1 to 0.5. The graph is scaled vertically toward the $x$ axis while its overall shape remains unchanged.

And so on.