Heine - Cantor Theorem

If a function \( f(x) \) is continuous on a closed and bounded interval [a, b], then it is uniformly continuous on [a, b].

The Heine - Cantor theorem provides a sufficient condition for uniform continuity.

In general, continuity does not imply uniform continuity.

However, when a function is continuous on a closed and bounded interval, this suffices to ensure it is also uniformly continuous.

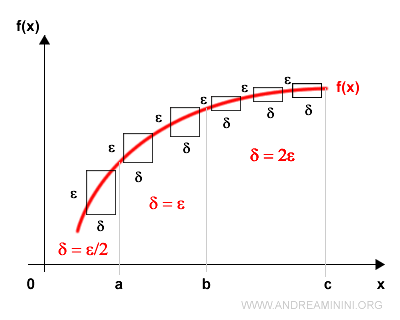
Explanation: On a closed interval [a, b], we seek a relationship \( \delta = \delta(\epsilon) \) that guarantees uniform continuity. Such a relationship is valid only within [a, b]; for other intervals, a different function \( \delta = \delta'(\epsilon) \) may be required. The only condition needed is that the function be continuous on the interval under consideration. For example, in the diagram above, the function is uniformly continuous on [b, c] with \( \delta = 2\epsilon \), and on [a, b] with \( \delta = \epsilon \). However, on [0, a], the function is only continuous, and satisfies \( \delta = \epsilon / 2 \). In this last case, uniform continuity fails near the right-hand neighborhood of 0, where the graph steepens dramatically. According to the Heine - Cantor theorem, to restore uniform continuity, we must restrict to a smaller subinterval, such as [0.5, a], where the function becomes uniformly continuous again with \( \delta = \epsilon / 3 \).

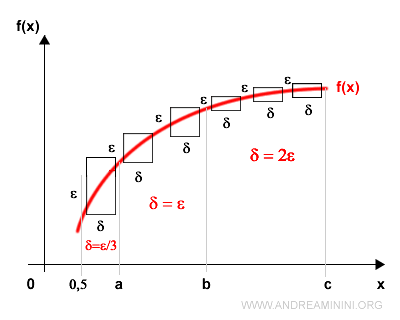
Conversely, on [0, 0.5], the function remains continuous but fails to be uniformly continuous. And so on.

Proof

The proof proceeds by contradiction.

Suppose there exists some \( \epsilon_0 > 0 \) such that, for every \( \delta > 0 \), one can find points \( x, x' \in [a, b] \) such that:

$$ \exists \epsilon_0 > 0 : \forall \delta > 0,\ \exists x,x' \in [a, b] \text{ such that } |x - x'| < \delta \text{ and } |f(x) - f(x')| \ge \epsilon_0 $$

This statement is the logical negation of the definition of uniform continuity.

Note: By definition, a function is uniformly continuous on [a, b] if: $$ \forall \epsilon > 0,\ \exists \delta > 0\ \text{ such that } \forall x,x' \in [a, b],\ |x - x'| < \delta \Rightarrow |f(x) - f(x')| \le \epsilon $$

Let us now choose \( \delta = 1/n \), with \( n \in \mathbb{N} \). Then the assumption becomes:

$$ \exists \epsilon_0 > 0 : \forall n \in \mathbb{N},\ \exists x_n, x_n' \in [a, b]\ \text{ such that } |x_n - x_n'| < \frac{1}{n},\ |f(x_n) - f(x_n')| \ge \epsilon_0 $$

By the Bolzano - Weierstrass theorem, the sequence \( x_n \) has a convergent subsequence \( x_{n_k} \). Because \( x_n' \) lies within \( 1/n \) of \( x_n \), it follows that:

$$ x_{n_k} - \frac{1}{n_k} < x_{n_k}' < x_{n_k} + \frac{1}{n_k} $$

Hence both \( x_{n_k} \) and \( x_{n_k}' \) converge to the same limit \( x_0 \in [a, b] \).

By the squeeze theorem, we have:

$$ \lim_{k \to \infty} x_{n_k}' = x_0 $$

Since \( f \) is continuous on [a, b], the limit of the difference must vanish:

$$ \lim_{k \to \infty} [f(x_{n_k}) - f(x_{n_k}')] = f(x_0) - f(x_0) = 0 $$

But this contradicts our earlier assumption that:

$$ |f(x_n) - f(x_n')| \ge \epsilon_0 $$

Therefore, the assumption must be false, and the theorem is established by contradiction.

And so on.