Inverse Function

What Is an Inverse Function?

Given a function $y = f(x)$, the inverse function $f^{-1}$ reverses this mapping, associating each element of the codomain $Y$ with a unique element in the domain $X$.

A function from $X$ to $Y$ is said to be invertible if there exists an inverse function from $Y$ to $X$.

If $f$ is a bijective function from $X$ to $Y$, then:

$$ f: X \rightarrow Y $$

its inverse function $f^{-1}$ is also bijective and defined as:

$$ f^{-1}: Y \rightarrow X $$

such that for every $y \in Y$, there exists a unique $x \in X$ with $y = f(x)$.

Note. The notation $f^{-1}$ denotes the inverse of the function $f$ - it does not mean $1/f$.

Not every function admits an inverse. Functions that do are called invertible functions.

Every bijective function - that is, every function that is both injective and surjective - is invertible.

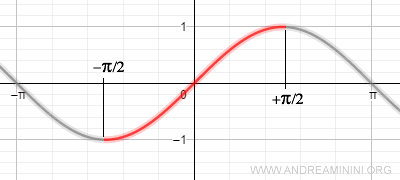
Note. Some functions may not be invertible over their entire domain but become invertible when restricted to a suitable subdomain. For example, the sine function is not bijective - and hence not invertible - over the entire real line. However, it becomes bijective if restricted to the interval $(-\pi/2, \pi/2)$, and its inverse is known as the arcsine function.

A Practical Example

Example 1

Consider the function $f(x) = x + 1$ and the sets:

$$ X = \{1, 2, 3\}, \quad Y = \{2, 3, 4\} $$

The function $f$ defines a relation $R$ that is a subset of the Cartesian product $X \times Y$:

$$ R = \{(1, 2), (2, 3), (3, 4)\} $$

In this case, each element of $X$ is uniquely mapped to an element in $Y$:

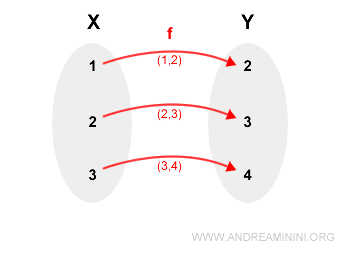
Note. The relation $f$ is a function because no first element is repeated in the ordered pairs.

The inverse relation $R^{-1}$ is:

$$ R^{-1} = \{(2, 1), (3, 2), (4, 3)\} $$

This inverse is also a function, as each first element appears only once:

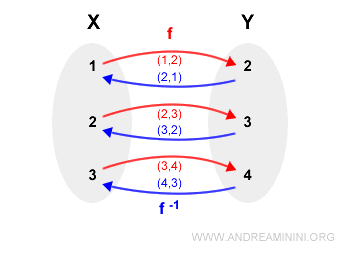
Thus, $f^{-1}$ is the inverse function of $f$, and $f$ is an invertible function.

Example 2

Now let:

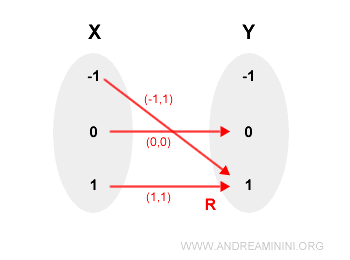
$$ X = \{-1, 0, 1\}, \quad Y = \{-1, 0, 1\} $$

Consider the relation defined by $y = x^2$, which produces:

$$ R = \{(-1, 1), (0, 0), (1, 1)\} $$

This is a valid function since no $x$ value is repeated:

However, the inverse relation $R^{-1}$ is:

$$ R^{-1} = \{(1, -1), (0, 0), (1, 1)\} $$

This is not a function, because the input 1 is associated with two different outputs:

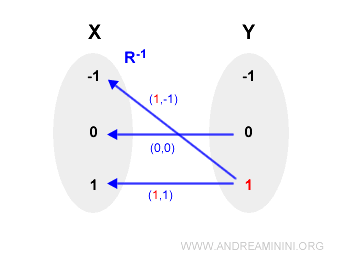
Therefore, the inverse of $f(x) = x^2$ over the domain $\{-1, 0, 1\}$ is not a function, and so $f$ is not invertible over this set.

Example 3

Consider the function $y = 2x - 1$:

$$ y = 2x - 1 $$

This is a bijective function, which means it is also invertible.

To find the inverse, we solve for $x$ in terms of $y$:

$$ 2x = y + 1 $$

$$ x = \frac{y + 1}{2} $$

In the inverse function, $y$ is treated as the independent variable, and $x$ becomes the dependent one.

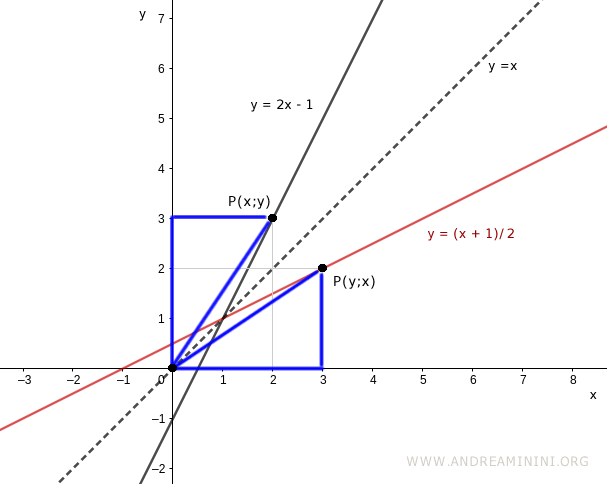
If we graph both the original function and its inverse on the same coordinate plane, their plots will be symmetric.

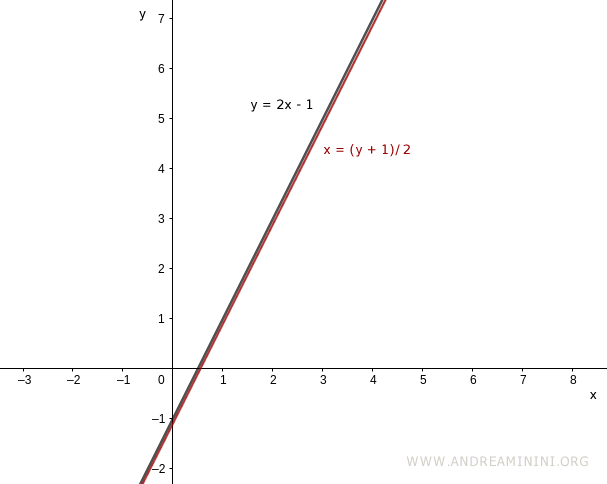
To represent the inverse using conventional axes, we interchange $x$ and $y$:

$$ y = \frac{x + 1}{2} $$

This allows us to plot both functions simultaneously on the same coordinate system:

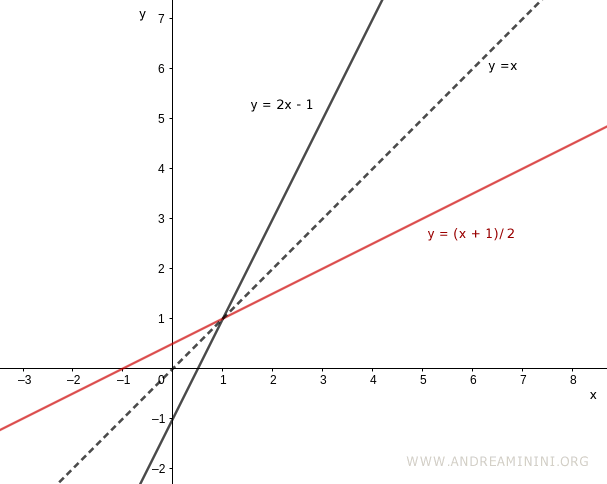
The graphs of $y = 2x - 1$ and its inverse $y = \frac{x + 1}{2}$ are mirror images of each other across the line $y = x$, which bisects the first and third quadrants.

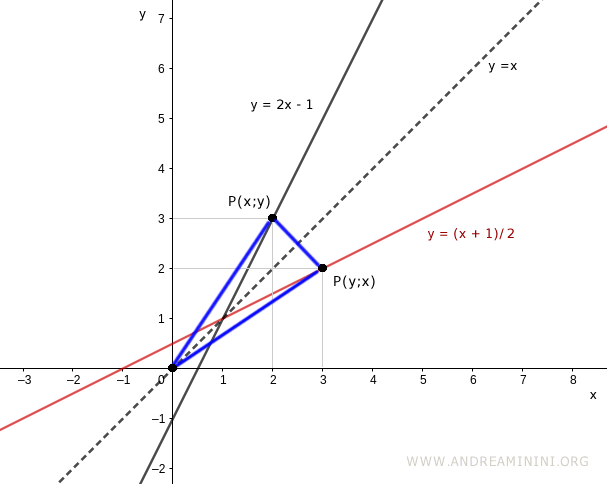
Note. If a point $P(x, y)$ lies on the graph of an invertible function, then the point $P(y, x)$ lies on the graph of its inverse. This symmetry holds because the two graphs are reflections across the line $y = x$.

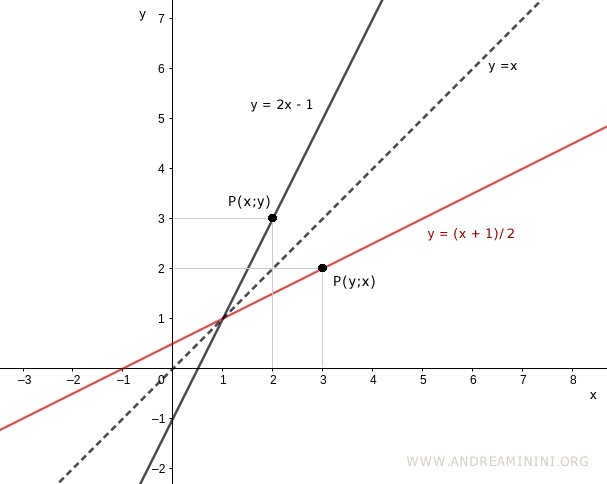
If you draw lines from each point to the origin and project them onto the axes, you form two congruent right triangles. This is a characteristic property of inverse functions.

Connecting the origin to both points also forms an isosceles triangle, illustrating the geometric symmetry.

Example 4

Now consider the function $y = x^2$, defined over the set of real numbers $\mathbb{R}$:

$$ y = x^2 \quad \text{for all } x \in \mathbb{R} $$

This function is not bijective, and therefore it is not invertible over its entire domain:

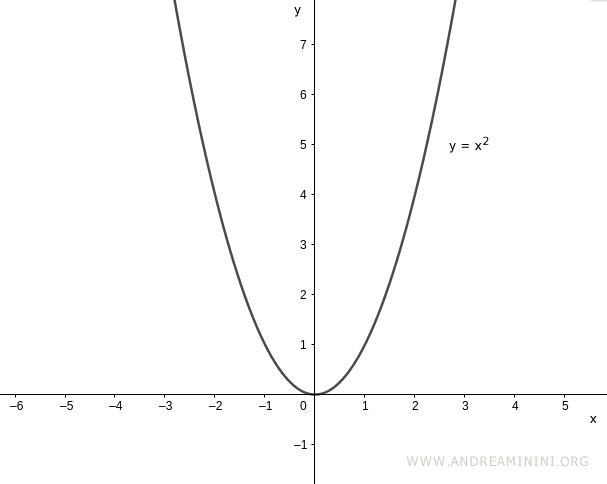
However, if we restrict the domain to the set of positive real numbers $\mathbb{R}^+$, the function becomes bijective:

$$ y = x^2 \quad \text{for all } x \in \mathbb{R}^+ $$

Over the interval $(0, \infty)$, the function $y = x^2$ is now invertible:

To determine the inverse, we take the square root of both sides and solve for $x$:

$$ \sqrt{y} = \sqrt{x^2} $$

$$ x = \sqrt{y} $$

To express the inverse in standard form, we switch the variables:

$$ y = \sqrt{x} $$

The graphs of the original function and its inverse are symmetric with respect to the line $y = x$:

Note. This example illustrates that a function which is not invertible over its full domain can become invertible when appropriately restricted to an interval where it is bijective.

Bijective Functions Are Invertible

If a function $f$ from $X$ to $Y$ is bijective, then it is also invertible.

A function is bijective (or a one-to-one correspondence) if it is both injective and surjective:

• Injective: Each element of the domain $X$ maps to a distinct element of the codomain $Y$.
• Surjective: Every element of the codomain $Y$ is the image of at least one element in the domain $X$.

Proof

Suppose $f(x)$ is a bijective function. Then:

$$ \text{domain}(f) = \text{codomain}(f^{-1}) = X $$

$$ \text{codomain}(f) = \text{domain}(f^{-1}) = Y $$

Assume that two ordered pairs share the same image:

$$ (x_1, y),\ (x_2, y) $$

Since $f$ is injective, it must be that:

$$ x_1 = x_2 $$

And because $f$ is also surjective, for every $y \in Y$ there exists exactly one $x \in X$ such that:

$$ (x, y) $$

Thus, the preimage of $y$ is unique and can be expressed as:

$$ x = f^{-1}(y) $$

This confirms that every bijective function admits an inverse and is therefore invertible.

Properties of Inverse Functions

The main properties of inverse functions include:

• If $f^{-1}$ is the inverse of $f$, then $f$ is also the inverse of $f^{-1}$.
• If $f^{-1}[f(x)] = x$, then $f[f^{-1}(y)] = y$.
• If $y = f(x)$ and $x = f^{-1}(y)$, then the two expressions are logically equivalent.

How to Find the Inverse of a Function

To determine the graph of the inverse function $f^{-1}(x)$ of an invertible function $f(x)$, you can use two graphical approaches or an analytical method.

Method 1: Reflection Across the Line $y = x$

Start by plotting the graph of the invertible function $f(x)$. For instance, consider $y = \log x$:

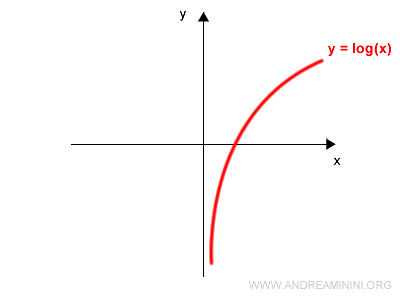
Next, draw the line $y = x$, which bisects the first and third quadrants. This is a straight line through the origin at a 45° angle:

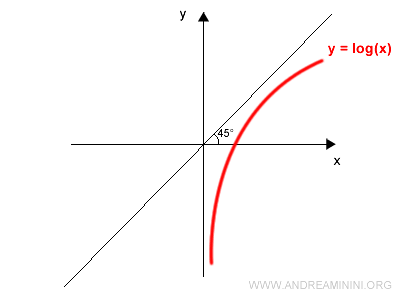
Reflect the graph of $f(x)$ across this line:

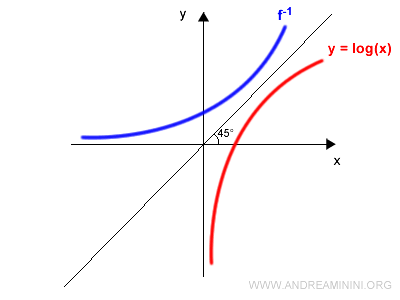
Then remove the original graph and relabel the axes by swapping $x$ and $y$:

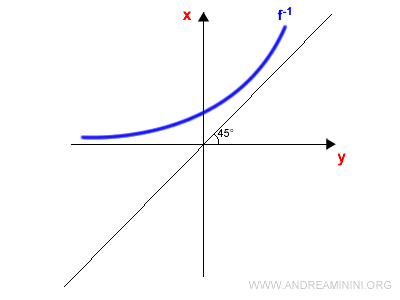
The resulting graph represents the inverse function $f^{-1}(x)$:

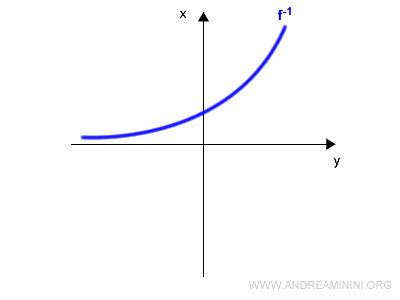
Method 2: Rotational Symmetry

Once again, plot the graph of an invertible function, such as $y = \log x$:

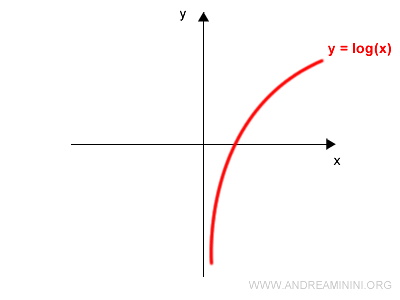
Now rotate the coordinate plane 90° counterclockwise: the $y$-axis moves to the left, and the $x$-axis points upward:

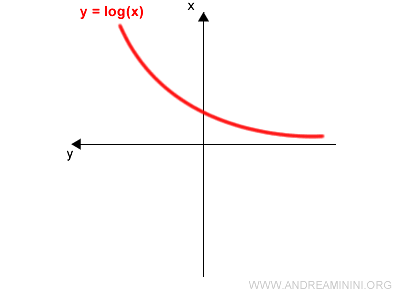
Next, perform a 180° rotation around the vertical axis:

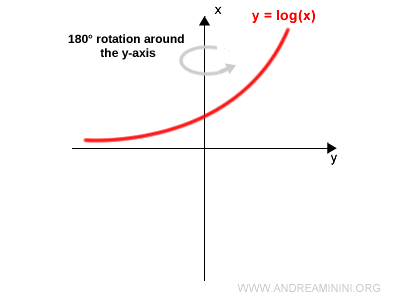
Note. This final transformation is equivalent to reflecting the graph across a vertical mirror. The result is the same.

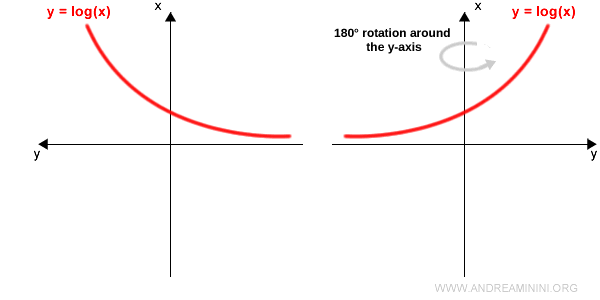
The resulting image is the graph of the inverse function $f^{-1}(x)$:

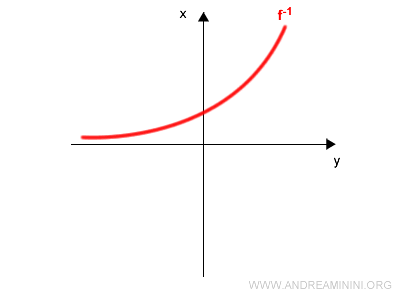
Method 3: Analytical Approach

To find the inverse of a function $y = f(x)$ analytically, solve the equation for $x$ in terms of $y$.

Let’s use the logarithmic function as an example:

$$ y = \log x $$

The corresponding graph is shown below:

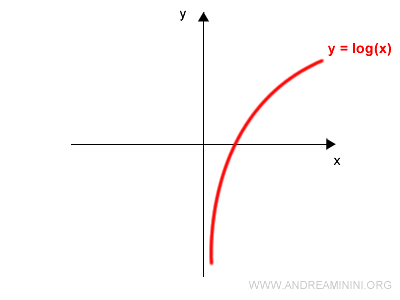
We now isolate $x$ by exponentiating both sides of the equation:

$$ e^y = e^{\log x} $$

Note. This step is valid because we apply the same algebraic operation to both sides of the equation.

Since $e^{\log x} = x$, it follows that:

$$ e^y = x $$

We have now expressed $x$ as a function of $y$. Thus, the inverse is:

$$ x = e^y $$

To write the inverse in standard form, we swap $x$ and $y$:

$$ y = e^x $$

The graph of the inverse exponential function looks like this:

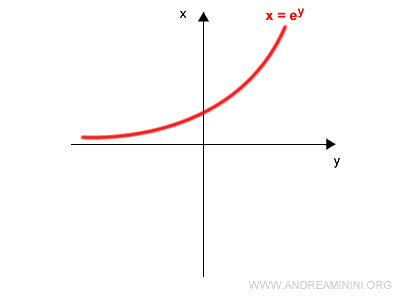
Note. This is the same result obtained using the graphical method described earlier on this page.

And so on.