Increasing and Decreasing Functions

A function that is consistently increasing or consistently decreasing on an interval \( I \) is said to be monotonic on \( I \).

Monotonicity concerns how the values of a function compare as the independent variable increases. It is a relational property between function values, not a qualitative description of the visual shape of the graph.

Example. This function f(x) is strictly increasing on the interval $ ( x_1,x_2) $ and strictly decreasing on the interval $ ( x_3 , x_4) $

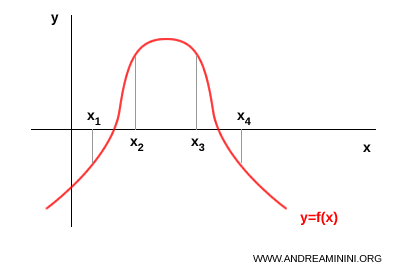
Monotonicity Criterion for Functions

To determine whether a function is increasing or decreasing, we can use the monotonicity criterion, which establishes a connection between the first derivative of a function f(x) and its growth or decline.

Increasing Function

A function f(x) that is continuous on [a, b] and differentiable on (a, b) is said to be increasing on [a, b] if its first derivative satisfies $$ f'(x) \ge 0 $$ for every x ∈ (a, b).

Decreasing Function

A function f(x) that is continuous on [a, b] and differentiable on (a, b) is said to be decreasing on [a, b] if its first derivative satisfies $$ f'(x) \le 0 $$ for every x ∈ (a, b).

Why Is This Important?

The sign of the first derivative f'(x) is one of the key pieces of information used in analyzing and sketching the graph of a function.

A Practical Example

Consider the function:

$$ f(x)=x^2 $$

The first derivative of the function is:

$$ f'(x)=2x $$

From -∞ to 0, the derivative f'(x)=2x is negative, whereas from 0 to +∞, it’s positive:

$$ f'(x)= \begin{cases} 2x > 0 \text{ if } x > 0 \\ 2x < 0 \text{ if } x < 0 \end{cases} $$

Therefore, the function f(x)=x² is decreasing on (-∞, 0) and increasing on (0, ∞).

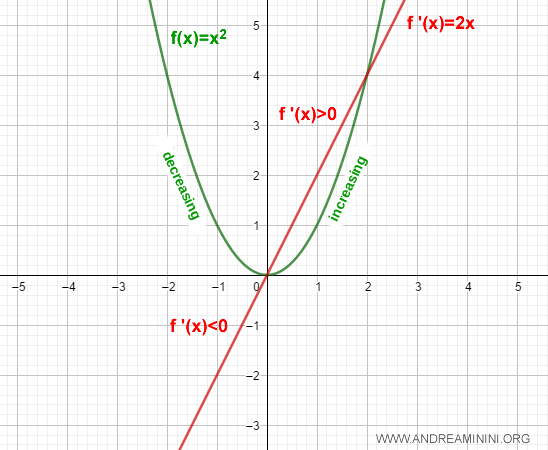
Proof and Explanation

Case 1 (Positive First Derivative)

Let’s start with the hypothesis that the first derivative f'(x) is nonnegative on the interval (a, b):

$$ f'(x) \ge 0 $$

We want to verify whether the function is indeed increasing.

Choose two points x₁ and x₂ in (a, b) such that:

$$ a \le x_1 \le x_2 \le b $$

If the function is increasing, then the following inequality should hold:

$$ f(a) \le f(x_1) \le f(x_2) \le f(b) $$

According to Lagrange’s Mean Value Theorem, there exists a point x₀ in the interval (x₁, x₂) such that:

$$ f'(x_0)=\frac{f(x_2)-f(x_1)}{x_2 - x_1} $$

Rewriting this, we have:

$$ f(x_2)-f(x_1) = f'(x_0)\,(x_2 - x_1) $$

Since f'(x₀) ≥ 0 by hypothesis, and (x₂ - x₁) > 0 because x₂ > x₁, it follows that:

$$ f(x_2)-f(x_1) \ge 0 $$

Hence, the function is increasing on the interval (x₁, x₂).

This establishes the connection between a nonnegative first derivative and an increasing function.

Note. The relationship between a nonpositive first derivative f'(x) ≤ 0 and a decreasing function f(x) can be proved similarly, assuming f'(x) ≤ 0. In that case, since (x₂ - x₁) > 0, we have f(x₂) - f(x₁) ≤ 0.

Case 2 (Function Increasing)

Now suppose that the function is increasing on the interval (a, b), without yet considering its derivative.

This means that at any point x₀ ∈ (a, b), the function is increasing.

To determine the derivative at x₀, we evaluate the limit of the difference quotient at that point:

$$ f'(x_0) = \lim_{h \rightarrow 0} \frac{f(x+h)-f(x)}{h} \ge 0 $$

Since the function is increasing, the numerator of the difference quotient satisfies:

• f(x+h) - f(x) ≥ 0 for h > 0
• f(x+h) - f(x) ≤ 0 for h < 0

Thus, the difference quotient is nonnegative for h > 0 (right-hand derivative):

$$ f'(x_0+) = \lim_{h \rightarrow 0} \frac{f(x+h)-f(x)}{h} \ge 0 $$

and also nonnegative for h < 0 (left-hand derivative):

$$ f'(x_0-) = \lim_{h \rightarrow 0} \frac{f(x+h)-f(x)}{h} \ge 0 $$

Note. For the left-hand derivative, the denominator h is negative (h < 0). Since the numerator f(x+h) - f(x) is also nonpositive, their ratio remains nonnegative.

Therefore, the first derivative of the function at x₀ is nonnegative:

$$ f'(x_0) \ge 0 $$

And so on.