Derivative and the Slope of the Tangent Line
The geometric interpretation of the derivative of a function f(x) is closely linked to the slope of the tangent line at a specific point on the curve. $$ f'(x_0) = \tan \:\: \alpha $$ where α represents the slope of the tangent line at the point f(x0).
Proof and Explanation
Let’s start by considering two points, A and B, on the graph of the function:
$$ f(x) $$
$$ f(x+h) $$
where h is the increment of the independent variable x.
The vertical distance between these two points is given by:
$$ f(x+h) - f(x) $$
Now, imagine locating point C at the intersection of lines drawn parallel to the coordinate axes through points A and B.
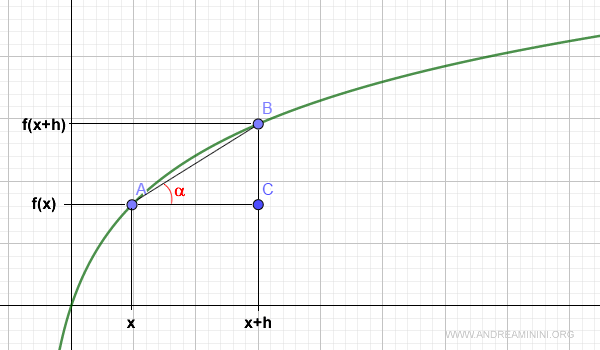
Connecting points A, B, and C forms a right triangle whose sides are:
- AC = h, which corresponds to Δx
- BC = f(x+h) - f(x), which corresponds to Δy
The difference quotient of the function between these two points is:
$$ \frac{f(x+h)-f(x)}{h} $$
This ratio represents the slope of the hypotenuse of the triangle, which is equivalent to &tan; α.
$$ \tan \:\: \alpha = \frac{f(x+h)-f(x)}{h} $$
Why is it equal to the tangent? By assuming AB = 1 (a unit radius), the ratio BC/AC in the right triangle corresponds to the ratio of sine to cosine in trigonometry.
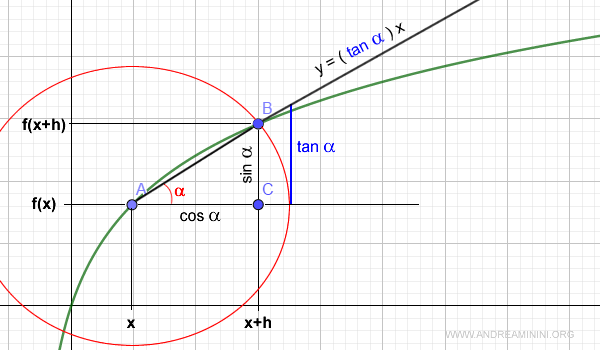
Since the ratio of sine to cosine equals the tangent, we have: $$ \frac{BC}{AC} = \frac{\sin \:\alpha}{\cos \:\alpha} = \tan \:\alpha $$
Therefore, the difference quotient (or tan α) also represents the slope of the line segment AB.
Example. Suppose AC = 6 and BC = 4. Then, the difference quotient is BC/AC, which is 4/6 = 2/3. Thus, the tangent of angle α equals 2/3.
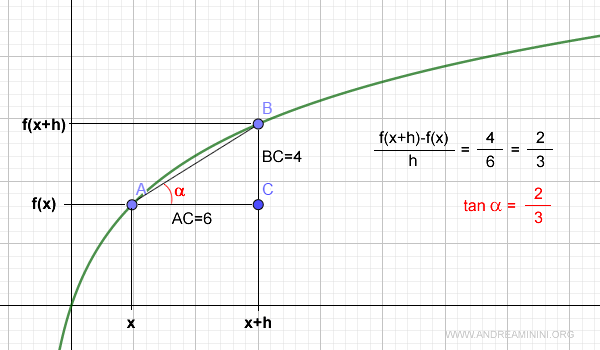
Tan α is also the slope of a line passing through points A and B. Therefore, segment AB is parallel to a line of the form y = (tan α) x passing through the origin, where alpha is the slope - in this case, y = (2/3)x.
If the function is differentiable at a point x, we can find the limit of the difference quotient as h approaches zero.
This yields the derivative of f(x) at the point x:
$$ \lim_{h \rightarrow 0} \frac{f(x+h)-f(x)}{h} = f'(x) $$
The limit of the difference quotient - the derivative - has an important geometric meaning.
It is equal to the slope β of the tangent line to the curve at the point x.
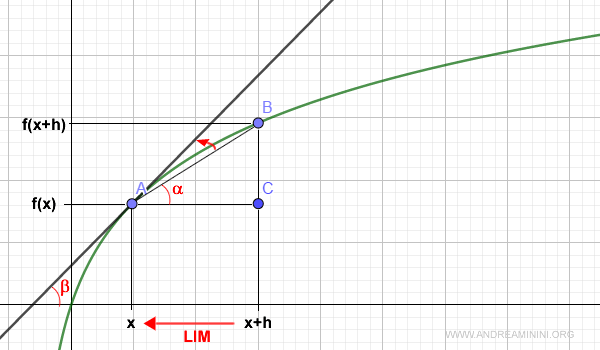
Therefore, the Cartesian equation of the tangent line takes the form:
$$ y = \beta \cdot x $$
More generally, we can state:
Given a point (x0, y0) on the function, the equation of the tangent line at x0 is: $$ y - y_0 = f'(x_0) \cdot (x - x_0) $$
This formula allows us to determine the equation of the tangent line at the point (x0, y0), except in the special case where the tangent is vertical.
To check whether a vertical tangent exists at a given point, a different method must be used.
Note. At a point x0 where the function is continuous, a vertical tangent exists if the limit of the derivative at x0 exists and equals +∞ or -∞.
A Simple Example
Let’s explore the function x2 as an example:
$$ f(x) = x^2 $$
We’ll consider the point x = 1 and choose an increment h = 1:
$$ f(x) = f(1) = 1 $$
$$ f(x+h) = f(1+1) = f(2) = 4 $$
This provides us with two points, A and B:
$$ A \begin{pmatrix} 1 \\ 1 \end{pmatrix}$$
$$ B \begin{pmatrix} 2 \\ 4 \end{pmatrix}$$
Next, we locate point C.
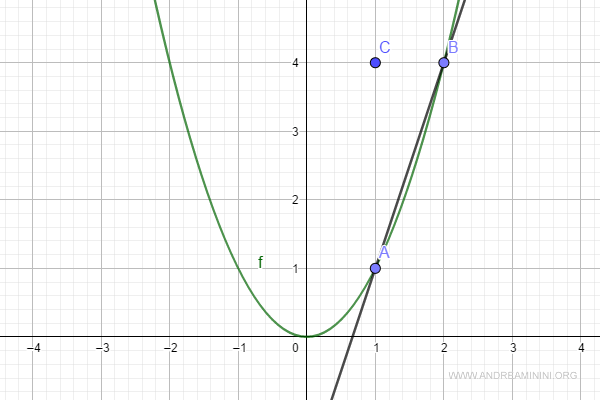
At this stage, we can calculate the difference quotient for the function:
$$ \frac{f(x+h)-f(x)}{h} = \frac{4-1}{1} = 3 $$
So, the difference quotient equals 3.
This means that the tangent of angle α is also 3:
$$ \tan \: \alpha = 3 $$
Consequently, the slope (m) of the line segment AB is 3.
To find the Cartesian equation of the line passing through points A and B, we use the point-slope form:
$$ y - y_0 = m \cdot (x - x_0) $$
Since we already know the slope (m = 3):
$$ y - y_0 = 3 \cdot (x - x_0) $$
We’ll take point A (1, 1) as our reference point (x0, y0):
$$ y - 1 = 3 \cdot (x - 1) $$
$$ y = 3x - 3 + 1 $$
$$ y = 3x - 2 $$
Hence, we’ve determined the Cartesian equation of the line passing through points A and B.
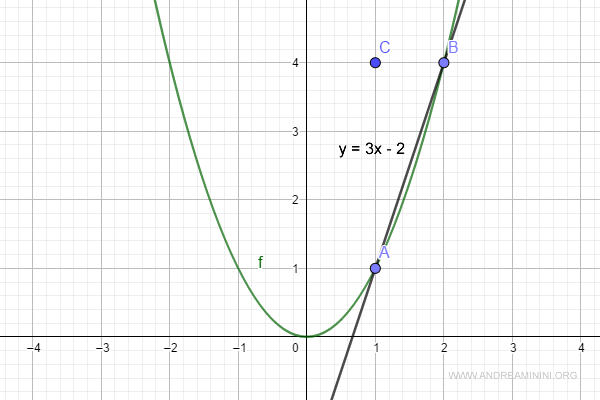
Now, we can evaluate the limit of the difference quotient as h approaches zero:
$$ \lim_{h \rightarrow 0} \frac{f(x+h)-f(x)}{h} = f'(x) $$
This limit gives us the first derivative f'(x) of the function f(x).
It also represents the tangent of angle α, which is the slope of the tangent line (r) at point A on the curve f(x).
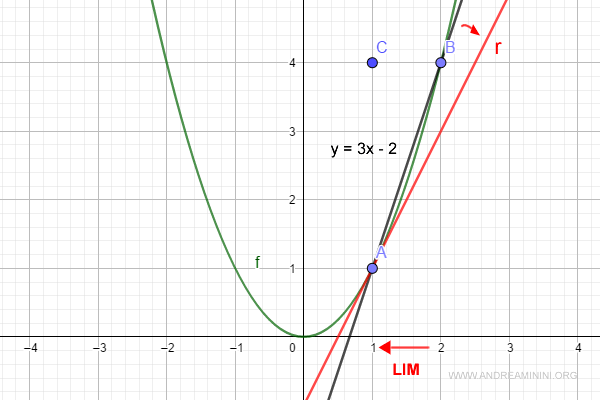
What is the equation of the tangent line?
In this case, we’re interested in a single point rather than two distinct points.
However, we already know that the limit of the difference quotient equals tan α, which is precisely the first derivative f'(x):
$$ \lim_{h \rightarrow 0} \frac{f(x+h)-f(x)}{h} = \tan \:\: \alpha = f'(x) $$
So, to find the slope of the tangent line, we simply need to know the derivative f'(x).
The derivative of f(x) = x2 is:
$$ f'(x) = 2x $$
At the point x = 1, the derivative f'(x) evaluates to 2:
$$ f'(1) = 2 \cdot 1 = 2 $$
Therefore, the slope of the tangent line at point A is 2.
To determine the equation of the tangent line, we again apply the point-slope formula:
$$ y - y_0 = m \cdot (x - x_0) $$
Since the slope is m = 2:
$$ y - y_0 = 2 \cdot (x - x_0) $$
Using point A (1, 1) as the reference point (x0, y0):
$$ y - 1 = 2 \cdot (x - 1) $$
$$ y = 2x - 2 + 1 $$
$$ y = 2x - 1 $$
Thus, we’ve established the Cartesian equation of the tangent line to f(x) at point A.
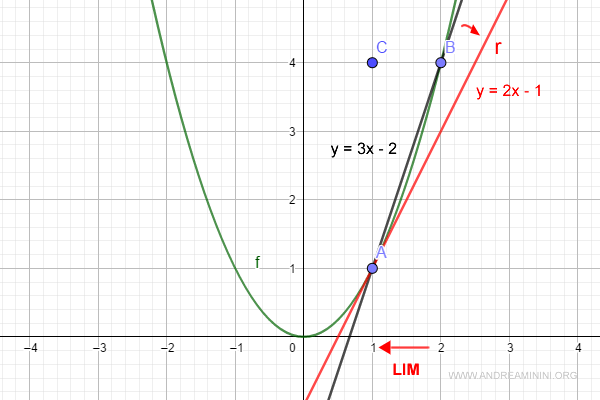
How do we find the tangent line at another point?
The approach remains the same.
We calculate the slope of the tangent line at the new point.
Then we construct the Cartesian equation of the tangent line using the coordinates of that point.
Example: the tangent line at point B
The line r′ is tangent to the curve at point B (shown in blue).
Its slope differs from that of the tangent line at point A (shown in red). The inclinations are not the same.
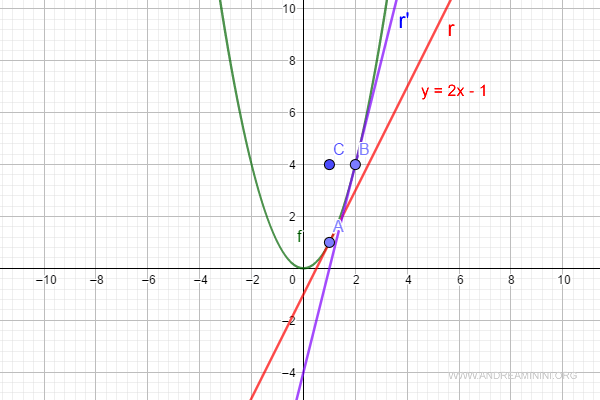
Although the first derivative f'(x) remains the same function, we now evaluate it at a different x-value (x = 2).
The slope of line r′ is 4:
$$ f'(x) = 2 \cdot x = \tan \: \alpha $$
$$ f'(2) = 2 \cdot 2 = 4 $$
Once we have the slope (m = 4), we can determine the Cartesian equation of line r′ using the same point-slope formula:
$$ y - y_0 = m \cdot (x - x_0) $$
$$ y - y_0 = 4 \cdot (x - x_0) $$
In this case, our reference point is B (2, 4):
$$ y - 4 = 4 \cdot (x - 2) $$
$$ y = 4x - 8 + 4 $$
$$ y = 4x - 4 $$
Hence, we’ve found the Cartesian equation of the tangent line at point B (shown in blue).
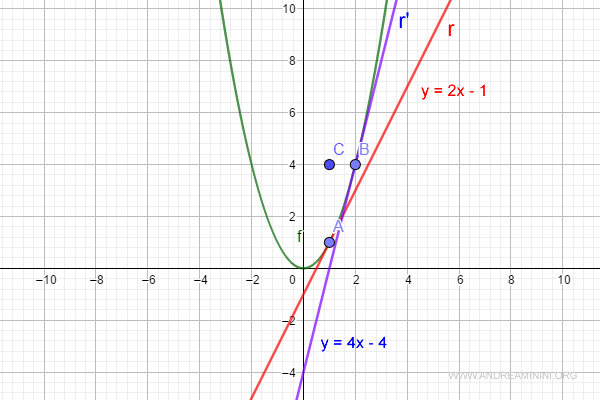
And so on.
