Derivative of the Square Root

The derivative of a square root is given by $$ D[\sqrt{x}] = \frac{1}{2 \cdot \sqrt{x}} $$

The Proof

Let’s prove this basic differentiation rule by considering the function:

$$ f(x) = \sqrt{x} $$

We look at the difference quotient:

$$ \lim_{h \rightarrow 0} \frac{f(x+h)-f(x)}{h} $$

where

$$ f(x)=\sqrt{x} $$

and

$$ f(x+h)=\sqrt{x+h} $$

Plugging these into the difference quotient gives us:

$$ \lim_{h \rightarrow 0} \frac{\sqrt{x+h}-\sqrt{x}}{h} $$

To simplify the difference quotient, we multiply the numerator and denominator by the conjugate:

$$ \lim_{h \rightarrow 0} \frac{\sqrt{x+h}-\sqrt{x}}{h} \cdot \frac{\sqrt{x+h}+\sqrt{x}}{\sqrt{x+h}+\sqrt{x}} $$

Expanding the numerator, we get:

$$ \lim_{h \rightarrow 0} \frac{\sqrt{x+h}\cdot (\sqrt{x+h}+\sqrt{x} ) -\sqrt{x} \cdot (\sqrt{x+h}+\sqrt{x})}{h \cdot \sqrt{x+h}+\sqrt{x} } $$

$$ \lim_{h \rightarrow 0} \frac{ \sqrt{x+h} \cdot \sqrt{x+h} + \sqrt{x+h} \cdot \sqrt{x} -\sqrt{x} \cdot \sqrt{x+h} - \sqrt{x} \sqrt{x})}{h \cdot \sqrt{x+h}+\sqrt{x} } $$

$$ \lim_{h \rightarrow 0} \frac{(x+h) + \sqrt{x^2+hx} - \sqrt{x^2+hx} -x}{h \cdot \sqrt{x+h}+\sqrt{x} } $$

$$ \lim_{h \rightarrow 0} \frac{h}{h \cdot \sqrt{x+h}+\sqrt{x} } $$

$$ \lim_{h \rightarrow 0} \frac{1}{ \sqrt{x+h}+\sqrt{x} } $$

Taking the limit as \( h \to 0 \), we find:

$$ \lim_{h \rightarrow 0} \frac{1}{ \sqrt{x+h}+\sqrt{x} } = \frac{1}{ \sqrt{x}+\sqrt{x} } = \frac{1}{ 2\sqrt{x} } $$

So, we’ve established the derivative of the square root of \( x \).

Graphical Representation

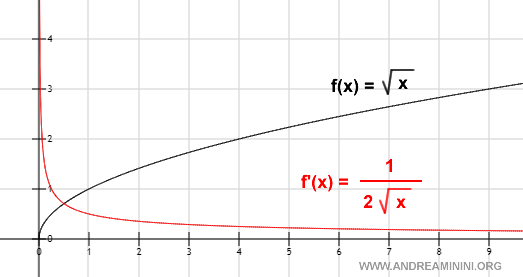
A Worked Example

Let’s calculate the derivative of the following function:

$$ f(x) = \sqrt{3x+1} $$

Note. When differentiating a square root, it’s crucial to be cautious: in many cases, it’s not just a matter of applying the basic derivative of a square root directly. For instance, here the derivative is NOT $$ \frac{1}{2 \sqrt{3x+1}} \:\:\: incorrect $$ $$ \frac{1}{2 \sqrt{3}} \:\:\: incorrect $$

In this case, we’re dealing with a composite function \( g[h(x)] \), where:

$$ g(x) = \sqrt{h(x)} $$

$$ h(x) = 3x+1 $$

This means we have to apply the chain rule.

The chain rule states:

$$ g'[h(x)] \cdot h'(x) $$

where

$$ g'[h(x)] = D[ \sqrt{h(x)} ] = \frac{1}{2\sqrt{h(x)}} = \frac{1}{2\sqrt{3x+1}} $$

and

$$ h'(x) = D[3x+1] = 3 $$

Putting it all together, we get:

$$ g'[h(x)] \cdot h'(x) = \frac{1}{2\sqrt{3x+1}} \cdot 3 = \frac{3}{2\sqrt{3x+1}} $$

Thus, the derivative of \( f(x) \) is:

$$ f'(x) = \frac{3}{2\sqrt{3x+1}} $$

And that’s the result.