Maxima and Minima Using Derivatives

The maximum and minimum values of a function f(x) can be analyzed through its derivatives.

If the first derivative is zero at x₀: $$ f'(x_0) = 0 $$ then the function exhibits:
• a local maximum if the second derivative is negative $$ f''(x_0) < 0 $$
• a local minimum if the second derivative is positive $$ f''(x_0) > 0 $$

General Criterion

This criterion for identifying minima and maxima can be extended as follows:

If the k-th derivative vanishes at x₀, and k is odd:

$$ f^{(k)}(x_0) = 0 \quad \text{with} \quad k \text{ odd} $$

Then the function has:

• a local maximum if the (k+1)-th derivative is negative $$ f^{(k+1)}(x_0) < 0 $$
• a local minimum if the (k+1)-th derivative is positive $$ f^{(k+1)}(x_0) > 0 $$
• neither a maximum nor a minimum if the (k+1)-th derivative is zero while the (k+2)-th derivative is nonzero $$ f^{(k+1)}(x_0) = 0 \:\: \text{and} \:\: f^{(k+2)}(x_0) \ne 0 $$ In such a case, the function has an inflection point.

Note. If the k-th derivative vanishes and k is even, then the function has neither a minimum nor a maximum at x₀, provided the (k+1)-th derivative is nonzero. In such points, the function instead possesses an inflection point.

Proof

To prove this criterion, we start with the Taylor series expansion of a function that is continuous and differentiable up to order n at x₀:

$$ f(x) = \sum_{k=0}^{n} \frac{f^{(k)}(x_0)}{k!} \cdot (x - x_0)^k + R_n(x) $$

which can be rewritten as:

$$ f(x) = f(x_0) + f^{(1)}(x_0) \cdot \frac{ (x - x_0)^1 }{1!} + f^{(2)}(x_0) \cdot \frac{ (x - x_0)^2 }{2!} + \dots + f^{(n)}(x_0) \cdot \frac{ (x - x_0)^n }{n!} + R_n $$

Suppose that all derivatives of the function up to order n - 1 vanish at x₀:

$$ f'(x_0) = f''(x_0) = f^{(3)}(x_0) = \dots = f^{(n-1)}(x_0) = 0 $$

Under these conditions, the Taylor expansion reduces to:

$$ f(x) = f(x_0) + f^{(n)}(x_0) \cdot \frac{ (x - x_0)^n }{n!} + R_n $$

Assuming that the n-th derivative is positive at x₀:

$$ f^{(n)}(x_0) > 0 $$

Note. The proof proceeds analogously if f⁽ⁿ⁾ were negative at x₀. In that case, the point would correspond to a local maximum rather than a minimum.

We now consider the following limit:

$$ \lim_{x \rightarrow x_0} \frac{f(x) - f(x_0)}{(x - x_0)^n} $$

Substituting from the reduced Taylor expansion yields:

$$ \lim_{x \rightarrow x_0} \frac{\left[ f(x_0) + f^{(n)}(x_0) \cdot \frac{ (x - x_0)^n }{n! } + R_n \right] - f(x_0)}{(x - x_0)^n} $$

$$ \lim_{x \rightarrow x_0} \frac{ f^{(n)}(x_0) \cdot \frac{ (x - x_0)^n }{n! } + R_n }{(x - x_0)^n} $$

$$ \lim_{x \rightarrow x_0} \left[ f^{(n)}(x_0) \cdot \frac{ (x - x_0)^n }{n! } + R_n \right] \cdot \frac{1}{(x - x_0)^n} $$

$$ \lim_{x \rightarrow x_0} \frac{ f^{(n)}(x_0) }{n! } + \frac{R_n}{(x - x_0)^n} = \frac{ f^{(n)}(x_0) }{n! } > 0 $$

Therefore, the original limit is strictly positive:

$$ \lim_{x \rightarrow x_0} \frac{f(x) - f(x_0)}{(x - x_0)^n} > 0 $$

At this stage, we distinguish between two scenarios depending on whether n is even or odd:

• If n is even, the denominator (x - x₀)ⁿ remains positive, implying that f(x) > f(x₀) in every neighborhood around x₀. Consequently, x₀ is a local minimum.
• If n is odd, the denominator (x - x₀)ⁿ changes sign to the right and left of x₀. Hence, x₀ cannot represent a local minimum.

In conclusion, the point x₀ is a local minimum only if f⁽ⁿ⁾ ≠ 0 and n is even.

A Practical Example

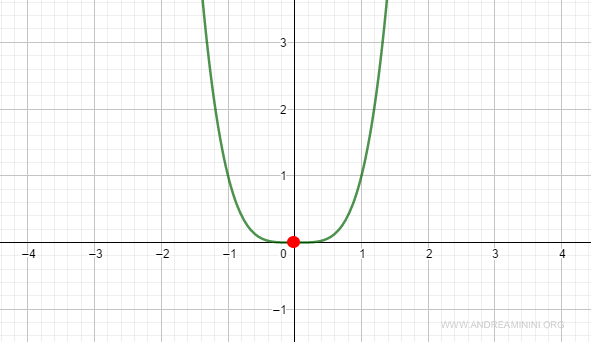
Example 1 (n even)

Consider the function:

$$ f(x) = x^4 $$

At x₀ = 0, the first, second, and third derivatives all vanish:

$$ f^{(1)}(x_0) = 4x^3 = 4(0)^3 = 0 $$

$$ f^{(2)}(x_0) = 12x^2 = 12(0)^2 = 0 $$

$$ f^{(3)}(x_0) = 24x = 24(0) = 0 $$

The fourth derivative, being even, is positive at x₀:

$$ f^{(4)}(x_0) = 24 > 0 $$

Thus, the function has a local minimum at x₀.

Example 2 (n odd)

Consider the function:

$$ f(x) = x^3 $$

At x₀ = 0, the first and second derivatives are zero:

$$ f^{(1)}(x_0) = 3x^2 = 3(0)^2 = 0 $$

$$ f^{(2)}(x_0) = 6x = 6(0) = 0 $$

The third derivative, which is odd, is positive:

$$ f^{(3)}(x_0) = 6 > 0 $$

In this situation, it is evident that the point does not correspond to a local minimum.

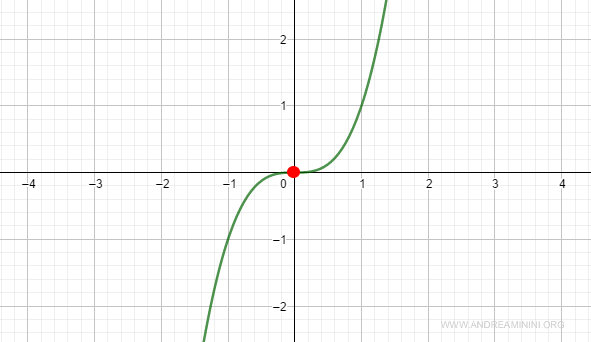
At x₀, the function has an inflection point.

And so on.