Fermat’s Theorem

If a function f(x) defined on the interval [a, b] attains a local maximum or minimum at the point x₀, then its first derivative at that point is zero. $$ f'(x_0)=0 $$

• It’s a local minimum if, in the neighborhood of x₀, the left-hand derivative is negative while the right-hand derivative is positive. $$ f'_-(x_0) < 0 \:\:\:, \:\:\: f'_+(x_0) > 0 $$
• It’s a local maximum if, near x₀, the left-hand derivative is positive and the right-hand derivative is negative. $$ f'_-(x_0) > 0 \:\:\:, \:\:\: f'_+(x_0) < 0 $$

Note. However, Fermat’s Theorem has a limitation: it applies only if x₀ is an interior point of the interval [a, b]. It cannot be used at the endpoints a or b, since derivatives can’t be computed in both directions there.

A Practical Example

Let’s examine the function f(x) defined over the real numbers:

$$ f(x)=x^2 $$

The first derivative of this function is:

$$ f'(x)=2x $$

The derivative equals zero only at the point x=0:

$$ f'(0)=0 $$

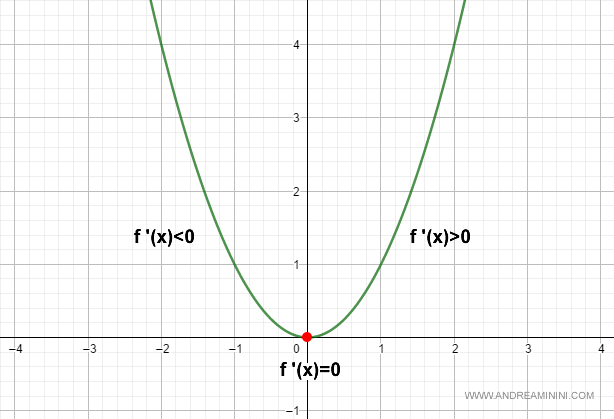
Thus, at x=0, the function has either a local maximum or a local minimum.

Is it a minimum or a maximum?

To determine which, we analyze the left-hand and right-hand derivatives around x₀=0:

$$ f'_-(0) < 0 $$

$$ f'_+(0) > 0 $$

Here, because the function is decreasing to the left (negative derivative) and increasing to the right (positive derivative), x₀ is a local minimum.

Note. Alternatively, if the function is twice differentiable, you can check the sign of the second derivative. If the second derivative is nonnegative, it indicates a minimum; if it’s nonpositive, it indicates a maximum.

Proof

If a function defined on [a, b] has a local maximum at x₀, then it must increase to the left of x₀ and decrease to the right.

This translates into the first derivative being positive on the left and negative on the right of x₀:

$$ f'_-(x_0) = \lim_{h \rightarrow 0^-} \frac{f(x_0+h)-f(x_0)}{h} \ge 0 $$

$$ f'_+(x_0) = \lim_{h \rightarrow 0^+} \frac{f(x_0+h)-f(x_0)}{h} \le 0 $$

According to the criteria for differentiability at a point, a function is differentiable at x₀ if its left-hand and right-hand derivatives are equal and coincide with f'(x₀).

Therefore, the derivative at x₀ must be zero, since it’s the only value shared by both one-sided derivatives.

$$ f'(x_0) = \lim_{h \rightarrow 0} \frac{f(x_0+h)-f(x_0)}{h} = 0 $$

Note. A similar argument holds for proving the existence of a local minimum. In that case, f(x) decreases to the left (negative left-hand derivative) and increases to the right (positive right-hand derivative) of x₀. If the function is differentiable at x₀, the first derivative must equal zero because it must match the values of both one-sided derivatives.

Local Extrema at the Endpoints

To determine whether an endpoint of an interval is a local maximum or minimum, we examine the one-sided derivative and the behavior of the function near that point. A point is a maximum if: $$ f'(x_0) \cdot (x - x_0) \le 0 $$ It’s a minimum if: $$ f'(x_0) \cdot (x - x_0) \ge 0 $$

Example

Consider the function f(x) defined on the interval [5, 10]:

$$ f(x)=2x $$

We want to check whether x=10 (the right endpoint B) is a local maximum.

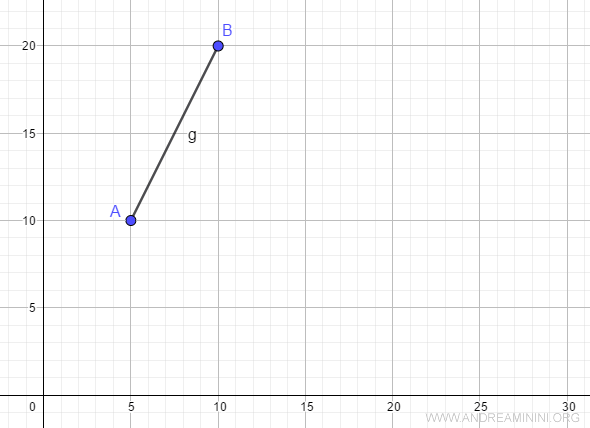
The right-hand derivative at f(10) does not exist because x=10 is the interval’s right endpoint.

However, the left-hand derivative at f(10) does exist and equals:

$$ f'_-(10)=2 $$

Applying the formula to assess the behavior of the function in the interval:

$$ f'(x_0) \cdot (x - x_0) $$

$$ 2 \cdot (x - 10) $$

Notice that for any x in the interval [5, 10], this expression is less than or equal to zero because (x - 10) is negative (or zero when x=10):

$$ 2 \cdot (x - 10) \le 0 $$

Therefore, the point x=10 is a local maximum.

Note. The same approach can be used to check whether the endpoint B is a local minimum. This method also applies to interior points, not just endpoints. For example, consider the function f(x)=sin x defined on the interval [1, 2]. Its derivative is f'(x)=cos x. We want to determine whether the point x=π/2 is a minimum, a maximum, or neither.

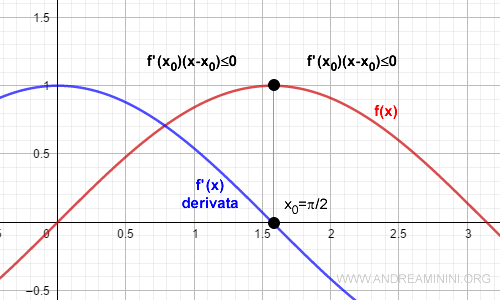
Let’s examine the neighborhood of x=π/2. To the left, the left-hand derivative f'_-(x₀)>0 and (x - x₀)<0. To the right, the right-hand derivative f'₊(x₀)<0 and (x - x₀)>0. In both cases, around x₀=π/2, the expression is always less than or equal to zero: $$ f'(x_0) \cdot (x - x_0) \le 0 $$ Thus, x=π/2 is a point of local maximum for the function f(x)=sin x.

And so on.