Strict Monotonicity Criterion

Strictly Increasing Function

A function that is continuous on [a,b] and differentiable on (a,b) is strictly increasing on [a,b] if its first derivative f'(x) is ≥ 0 for all x ∈ [a,b], and f'(x) does not remain zero throughout any interval within [a,b]. $$ \begin{cases} \forall x \in [a,b] \:\: | \:\: f'(x) \ge 0 \\ \forall (x_1,x_2) \subset (a,b) \:\: | \:\: f'(x) \ne 0 \end{cases} $$

Strictly Decreasing Function

A function that is continuous on [a,b] and differentiable on (a,b) is strictly decreasing on [a,b] if its first derivative f'(x) is ≤ 0 for all x ∈ [a,b], and f'(x) does not remain zero throughout any interval within [a,b]. $$ \begin{cases} \forall x \in [a,b] \:\: | \:\: f'(x) \le 0 \\ \forall (x_1,x_2) \subset (a,b) \:\: | \:\: f'(x) \ne 0 \end{cases} $$

Can the derivative of a strictly increasing or decreasing function be zero?

The derivative of a strictly increasing or strictly decreasing function may indeed be zero at a single point (e.g. f'(x₀) = 0), but it cannot remain zero across an entire interval of points.

A Practical Example

Example 1

The function f(x) = log x is strictly increasing on the interval [0, ∞) because its derivative f'(x) is ≥ 0, and it does not remain zero over any interval.

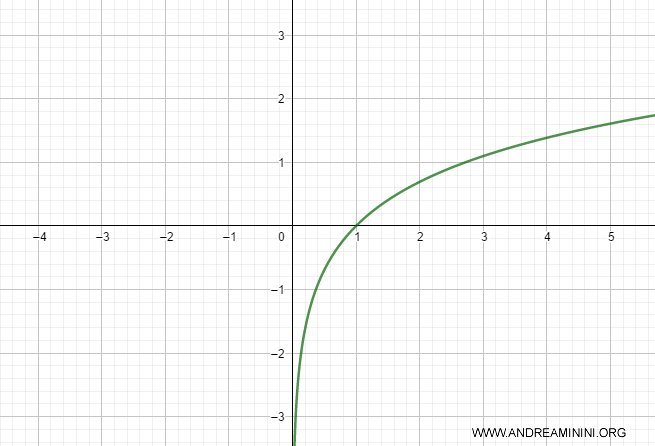
Example 2

The function f(x) = x³ is strictly increasing on the interval [0, ∞) because its derivative f'(x) is ≥ 0, and it does not remain zero over any interval.

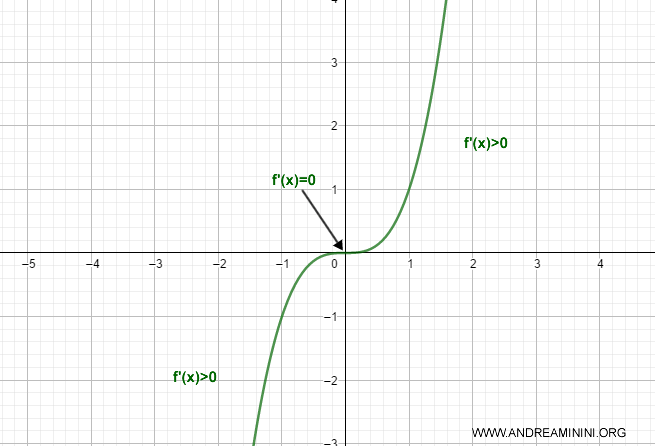
Note. At the point x = 0, the first derivative of the function is zero, f'(x) = 0. However, the function remains strictly increasing because this does not violate the strict monotonicity criterion. According to the criterion, the derivative cannot be identically zero across an interval.

Proof

1] Let’s start with a function f(x) such that f'(x) ≥ 0 for all x ∈ [a,b] and f'(x) ≠ 0 on every interval. We want to show that the function is strictly increasing.

$$ \begin{cases} \forall x \in [a,b] \:\: | \:\: f'(x) \ge 0 \\ \forall (x_1,x_2) \subset (a,b) \:\: | \:\: f'(x) \ne 0 \end{cases} \Rightarrow \text{strictly increasing} $$

If the function were not strictly increasing, there would exist two points x₁ < x₂ such that:

$$ f(x_1)=f(x_2) $$

Within the interval (x₁, x₂), the function would therefore be constant, according to the monotonicity criterion.

But this would contradict one of our initial assumptions:

$$ \forall x \in [x_1, x_2] \:\: | \:\: f'(x) = 0 $$

Therefore, the initial conditions imply that the function must indeed be strictly increasing.

Note. The points x₁ and x₂ do not need to be adjacent. Because f(x) is assumed to be increasing, it must remain constant throughout the interval (x₁, x₂) if it takes the same value at both endpoints. It cannot assume a value either higher or lower within the interval without violating the condition of being increasing on (a,b).

2] Now, assuming that the function is strictly increasing, we need to show that its derivative satisfies f'(x) ≥ 0 for every x ∈ [a,b], and that f'(x) is not zero throughout any interval (x₁, x₂) ⊂ [a,b].

$$ \text{strictly increasing} \Rightarrow \begin{cases} \forall x \in [a,b] \:\: | \:\: f'(x) \ge 0 \\ \forall (x_1,x_2) \subset (a,b) \:\: | \:\: f'(x) \ne 0 \end{cases} $$

If the derivative were negative, i.e. f'(x) < 0 at any point in [a,b], the function would not be increasing, and certainly not strictly increasing.

Therefore, the derivative must be non-negative everywhere:

$$ \forall x \in [a,b] \:\: | \:\: f'(x) \ge 0 $$

If the derivative were zero throughout an interval [x₁, x₂], then the function would be constant over that interval, given the assumption that the function is increasing. This would violate the condition of strict monotonicity.

Therefore, the derivative must necessarily be nonzero over every interval:

$$ \forall (x_1,x_2) \subset (a,b) \:\: | \:\: f'(x) \ne 0 $$

And so on.