Derivative of the Arctangent Function

The derivative of the arctangent function is given by: $$ D[\arctan x] = \frac{1}{1 + x^2}. $$

This result follows from the fact that the arctangent function is the inverse of the tangent function.

Thus, we can apply the inverse function differentiation rule.

Proof and Explanation

The tangent function is a continuous trigonometric function, but it is not monotonic across the entire set of real numbers:

$$ f(x) = \tan x $$

However, when restricted to the open interval $(-\pi/2, \pi/2)$, the tangent function is strictly increasing and monotonic.

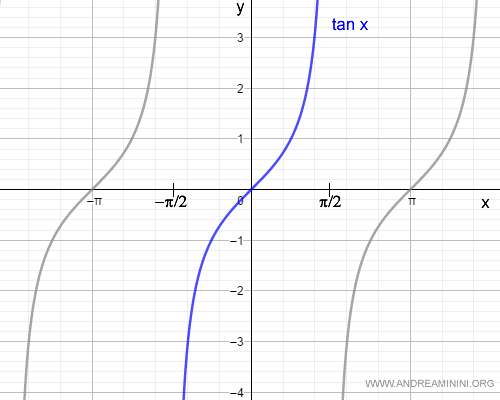
Therefore, within the interval $(-\pi/2, \pi/2)$, $\tan x$ is invertible, and its inverse function is the arctangent:

$$ f^{-1}\bigl(y = \tan x\bigr) = \arctan x $$

What is the arctangent? Geometrically, the arctangent represents the angle $\alpha$ (in radians or degrees) on the unit circle corresponding to a given tangent value.

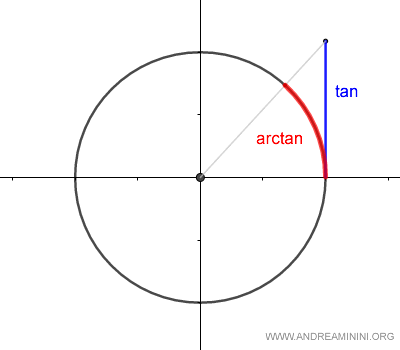
Thus, the tangent and arctangent are inverse functions of each other:
$$ y = \tan \alpha $$ $$ \alpha = \arctan y $$ Therefore, $$ y = \tan(\arctan y) $$ and $$ \alpha = \arctan(\tan \alpha). $$

The domain of the arctangent function is the entire real line $\mathbb{R}$, and its range (codomain) is the interval $(-\pi/2, \pi/2)$.

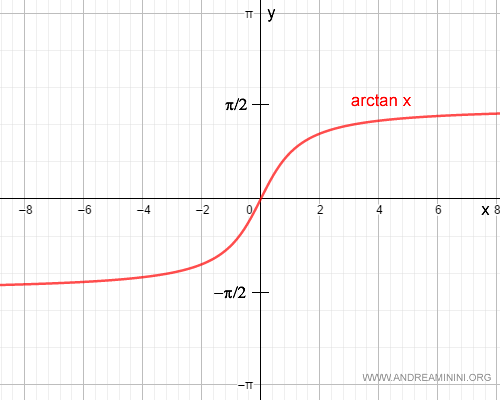
The limits of the arctangent function at positive and negative infinity are:

$$ \lim_{x \to +\infty} \arctan x = \frac{\pi}{2} $$

$$ \lim_{x \to -\infty} \arctan x = -\frac{\pi}{2} $$

Therefore, the arctangent function is differentiable for all real values of $x$.

To find its derivative, we apply the inverse function differentiation rule:

$$ D[f^{-1}(y)] = \frac{1}{D[f(y)]}. $$

Thus:

$$ D[\arctan x] = \frac{1}{D[\tan y]}. $$

The derivative of the tangent function is $1/\cos^2 y$:

$$ D[\arctan x] = \frac{1}{\frac{1}{\cos^2 y}}. $$

Note. Using the Pythagorean identity $\cos^2 y + \sin^2 y = 1$, we can express the denominator as $\cos^2 y + \sin^2 y$.

$$ D[\arctan x] = \frac{1}{\frac{\cos^2 y + \sin^2 y}{\cos^2 y}}. $$

$$ D[\arctan x] = \frac{1}{\frac{\cos^2 y}{\cos^2 y} + \frac{\sin^2 y}{\cos^2 y}}. $$

$$ D[\arctan x] = \frac{1}{1 + \frac{\sin^2 y}{\cos^2 y}}. $$

Note. Since $\tan y = \sin y / \cos y$, squaring both sides gives $\tan^2 y = \sin^2 y / \cos^2 y$.

$$ D[\arctan x] = \frac{1}{1 + \tan^2 y}. $$

Note. Given that $y = \arctan x$:

$$ D[\arctan x] = \frac{1}{1 + \tan^2(\arctan x)}. $$

Note. Since the tangent and arctangent are inverse functions: $$ y = \arctan x \quad \text{and} \quad x = \tan y, $$ it follows that $$ \tan(\arctan x) = x. $$ Hence, $$ \tan^2(\arctan x) = x^2. $$

Therefore:

$$ D[\arctan x] = \frac{1}{1 + x^2}. $$

This completes the proof of the derivative formula for the arctangent function.

And so on.