Derivative of the Arcsine Function

The derivative of the arcsine function is: $$ D[\arcsin x] = \frac{1}{\sqrt{1 - x^2}}. $$

This result follows from the fact that the arcsine function is the inverse of the sine function.

Note. In trigonometry, the arcsine function (arcsin) is defined as the inverse of the sine function on the interval [-π/2, π/2].

Understanding the Arcsine Function

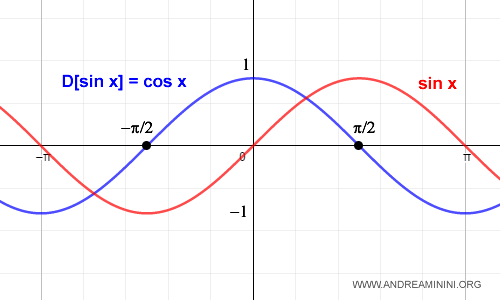
The sine function is not monotonic over its entire domain of real numbers.

However, it becomes a continuous and monotonic function when restricted to the interval [-π/2, π/2].

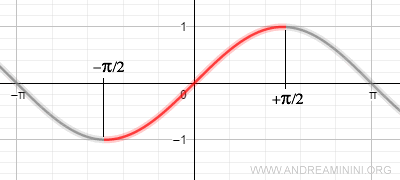
Within this interval, the sine function attains all values between its minimum of -1 and its maximum of 1.

Because it is continuous and monotonic on [-π/2, π/2], the sine function is also invertible there.

The inverse function of sine is known as the arcsine function:

$$ f^{-1}(x) = \arcsin x $$

Why is it called arcsine? It’s called arcsine because it represents the arc length $x$ on the unit circle - that is, the angle in radians whose sine equals a given value.

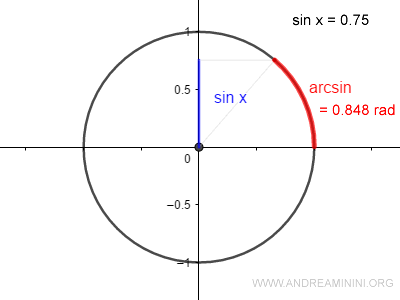
Since sine and arcsine are inverse functions of each other: $$ y = \sin x \\ x = \arcsin y $$ Therefore: $$ y = \sin(\arcsin y) \\ x = \arcsin(\sin x) $$

The domain of the independent variable of the arcsine function is the closed interval [-1, 1].

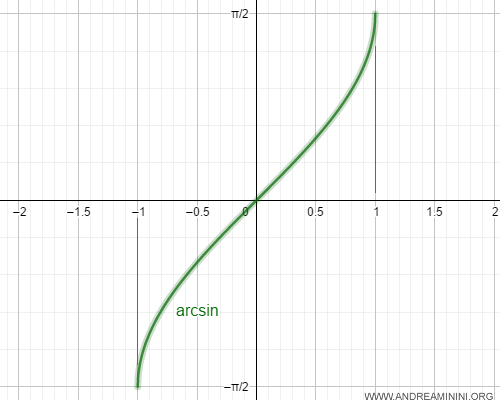
Thus, the arcsine function is differentiable on the open interval (-1, 1).

The Proof and Explanation

The arcsine function is the inverse of the sine function.

$$ f^{-1}(f(y)) = \arcsin x $$

Where $f(y)$ is defined as:

$$ f(y) = \sin y $$

Therefore, we can apply the inverse function differentiation rule:

$$ D[f^{-1}] = \frac{1}{D[f(y)]}. $$

So, for the arcsine function:

$$ D[\arcsin x] = \frac{1}{D[\sin y]}. $$

Since the derivative of sine is cosine, we have:

$$ D[\arcsin x] = \frac{1}{\cos y}. $$

Note. Recall the trigonometric identity: $$ \cos y = \sqrt{1 - \sin^2 y}. $$

Thus:

$$ D[\arcsin x] = \frac{1}{\sqrt{1 - \sin^2 y}}. $$

Note. Since $$ y = \arcsin x, $$ it follows that $$ \sin y = \sin(\arcsin x) = x. $$ Therefore, we can substitute and express the derivative entirely in terms of $x$: $$ \sin^2 y = \sin^2(\arcsin x) = x^2. $$

Hence:

$$ D[\arcsin x] = \frac{1}{\sqrt{1 - x^2}}. $$

This completes the proof of the derivative formula for the arcsine function.

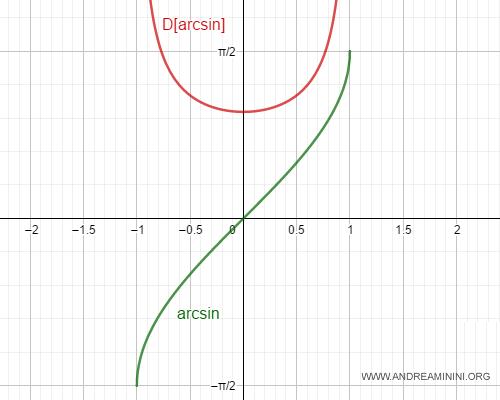
Note. The arcsine function is not differentiable at $x = 1$ and $x = -1$, since $\arcsin(1) = \pi/2$ and $\arcsin(-1) = -\pi/2$. At these points, the sine function equals $\pm 1$: $$ \sin(\pi/2) = 1 \\ \sin(-\pi/2) = -1 $$ The derivative of sine is cosine, and at these points the cosine value is zero: $$ \cos(\pi/2) = 0 \\ \cos(-\pi/2) = 0 $$

As a result, the derivative of the arcsine function is undefined at $x = \pm 1$, creating a vertical asymptote at those points.

And so on.