Finding Maxima and Minima Using Derivatives

The maxima and minima of a function f(x) can be analyzed through its derivatives.

If the first derivative equals zero at x₀: $$ f'(x_0) = 0 $$ then the function has:
• a local maximum if the second derivative is negative: $$ f″(x_0) < 0 $$
• a local minimum if the second derivative is positive: $$ f″(x_0) > 0 $$

The General Criterion

The test for determining whether a point is a minimum or maximum can be generalized as follows:

If the k-th derivative is zero at x₀ and k is odd:

$$ f^{(k)}(x_0) = 0 \quad \text{where } k \text{ is odd} $$

Then the function has:

• a local maximum if the (k+1)-th derivative is negative: $$ f^{(k+1)}(x_0) < 0 $$
• a local minimum if the (k+1)-th derivative is positive: $$ f^{(k+1)}(x_0) > 0 $$
• neither a maximum nor a minimum if the (k+1)-th derivative is zero but the (k+2)-th derivative is nonzero: $$ f^{(k+1)}(x_0) = 0 \quad \text{and} \quad f^{(k+2)}(x_0) \ne 0 $$ In this case, the function has an inflection point at x₀.

Note. If the k-th derivative is zero and k is even, then the function has neither a maximum nor a minimum at x₀ if the (k+1)-th derivative is nonzero. In such cases, the function has an inflection point.

Proof

To prove this criterion, we begin with the Taylor expansion of a function that is continuous and differentiable up to order n at x₀:

$$ f(x) = \sum_{k=0}^{n} \frac{f^{(k)}(x_0)}{k!} \cdot (x - x_0)^k + R_n(x) $$

Expanded explicitly, this reads:

$$ f(x) = f(x_0) + f^{(1)}(x_0) \cdot \frac{(x - x_0)}{1!} + f^{(2)}(x_0) \cdot \frac{(x - x_0)^2}{2!} + \ldots + f^{(n)}(x_0) \cdot \frac{(x - x_0)^n}{n!} + R_n $$

Suppose all derivatives up to order n-1 vanish at x₀:

$$ f'(x_0) = f″(x_0) = f^{(3)}(x_0) = \ldots = f^{(n-1)}(x_0) = 0 $$

Then the Taylor series simplifies to:

$$ f(x) = f(x_0) + f^{(n)}(x_0) \cdot \frac{(x - x_0)^n}{n!} + R_n $$

Suppose further that the n-th derivative at x₀ is positive:

$$ f^{(n)}(x_0) > 0 $$

This suggests a local minimum at x₀.

Note. The argument is similar if f⁽ⁿ⁾ is negative, in which case the point would be a local maximum instead of a minimum.

Consider the following limit:

$$ \lim_{x \rightarrow x_0} \frac{f(x) - f(x_0)}{(x - x_0)^n} $$

Substituting the Taylor series yields:

$$ \lim_{x \rightarrow x_0} \frac{\left[ f(x_0) + f^{(n)}(x_0) \cdot \frac{(x - x_0)^n}{n!} + R_n \right] - f(x_0)}{(x - x_0)^n} $$

which simplifies to:

$$ \lim_{x \rightarrow x_0} \frac{f^{(n)}(x_0)}{n!} + \lim_{x \rightarrow x_0} \frac{R_n}{(x - x_0)^n} = \frac{f^{(n)}(x_0)}{n!} > 0 $$

Therefore, the original limit is positive:

$$ \lim_{x \rightarrow x_0} \frac{f(x) - f(x_0)}{(x - x_0)^n} > 0 $$

We now distinguish between the cases when n is even or odd:

• If n is even, the denominator (x - x₀)ⁿ is always positive. Therefore, f(x) > f(x₀) for all x in some neighborhood (x₀ - δ, x₀ + δ). Hence, x₀ is a local minimum.
• If n is odd, the denominator (x - x₀)ⁿ changes sign on either side of x₀, so x₀ cannot be a local minimum.

In conclusion, x₀ is a minimum if and only if f⁽ⁿ⁾ ≠ 0 and n is even.

A Practical Example

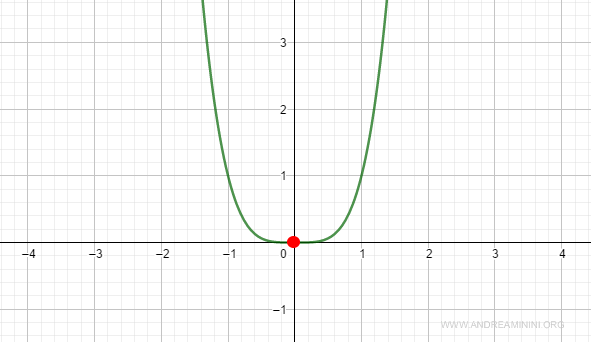
Example 1 (n even)

Consider the function:

$$ f(x) = x^4 $$

At the point x₀=0, the first, second, and third derivatives are zero:

$$ f^{(1)}(x_0) = 4x^3 = 4(0)^3 = 0 $$

$$ f^{(2)}(x_0) = 12x^2 = 12(0)^2 = 0 $$

$$ f^{(3)}(x_0) = 24x = 24(0) = 0 $$

The fourth derivative, which is even, is positive at x₀:

$$ f^{(4)}(x_0) = 24 > 0 $$

Thus, the function has a local minimum at x₀.

Example 2 (n odd)

Consider the function:

$$ f(x) = x^3 $$

At x=0, both the first and second derivatives vanish:

$$ f^{(1)}(x_0) = 3x^2 = 3(0)^2 = 0 $$

$$ f^{(2)}(x_0) = 6x = 6(0) = 0 $$

However, the third derivative, which is odd, is positive:

$$ f^{(3)}(x_0) = 6 > 0 $$

It’s clear in this case that the point is not a minimum.

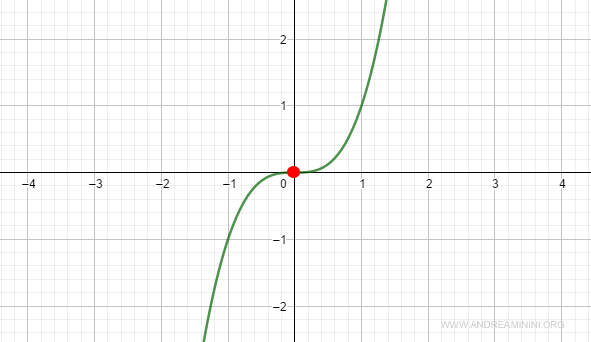
At x₀, the function has a point of inflection.

And so on.