Rolle’s Theorem

If a function f(x) is continuous on [a,b] and differentiable on (a,b), and if f(a) = f(b), then there is at least one point x₀ in (a,b) where the first derivative satisfies f'(x₀) = 0.

Proof

Let’s consider a function that’s continuous on [a,b] and differentiable on (a,b). By the properties of continuous functions, it must attain both a minimum (at x₁) and a maximum (at x₂) somewhere in the interval.

$$ f(x_1) \le f(x) \le f(x_2) $$

To prove that there’s at least one point where the derivative equals zero, we examine two possible scenarios:

1) Interior minimum or maximum within the interval

If at least one of the extreme values (the maximum at x₂ or the minimum at x₁) occurs strictly inside the interval (a,b), then by Fermat’s Theorem, the derivative at that point must be zero.

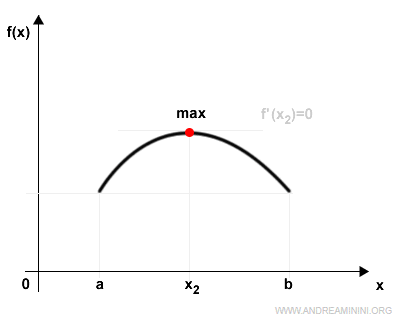
So, in this case, there’s at least one point x in (a,b) where f '(x) = 0.

2) Minimum and maximum occur at the endpoints

On the other hand, if both the minimum (x₁) and the maximum (x₂) fall at the endpoints of the interval, meaning they’re not interior points, then:

$$ f(x_1) = f(a) \\ f(x_2) = f(b) $$

Given that, by hypothesis, the function has the same value at both endpoints, we have:

$$ f(a) = f(b) $$

Hence, the minimum and the maximum must be equal:

$$ f(x_1) = f(x_2) $$

Since the minimum and maximum values coincide, the function must take that same constant value throughout the entire interval (a,b):

$$ f(x_1) \le f(x) \le f(x_2) $$

$$ f(x_1) = f(x) = f(x_2) $$

If f(x) is constant at every point x in (a,b), then the derivative f '(x) is zero everywhere in that interval.

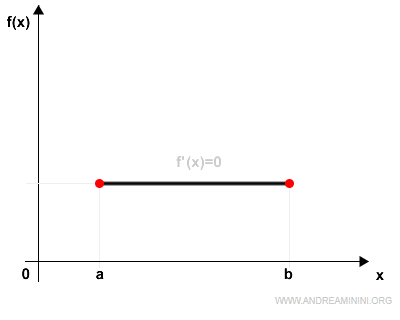
In this situation, there are infinitely many points in (a,b) where the derivative f '(x) equals zero.

This completes the proof that, if f(a) = f(b), there must exist at least one point in the interval (a,b) where f '(x) = 0.

And so on.