Derivative of a Power Function

Definition

The differentiation rule for power functions states: $$ D[ax^b]=b \cdot a x^{b-1} $$

To illustrate how this fundamental rule works, let’s walk through a formal proof and some practical examples.

Proof

Proof by Induction

Consider first the base case where n = 1. The derivative of x¹ is:

$$ D[x^1] = 1 \cdot x^0 = 1 $$

Suppose now that the differentiation rule holds for an arbitrary positive integer exponent n = k:

$$ D[x^k] = k \cdot x^{k-1} $$

We want to prove that the rule also holds for n = k + 1.

$$ D[x^{k+1}] $$

Observe that x^k+1 can be expressed as a product:

$$ D[x \cdot x^k] $$

Applying the product rule of differentiation gives:

$$ D[x \cdot x^k] = 1 \cdot x^k + x \cdot k \cdot x^{k-1} $$

Simplifying, we get:

$$ D[x \cdot x^k] = x^k + k \cdot x^k $$

$$ D[x \cdot x^k] = (1 + k) \cdot x^k $$

This confirms the rule holds for k + 1.

Therefore, by induction, the power rule is proven for all positive integer exponents.

Example

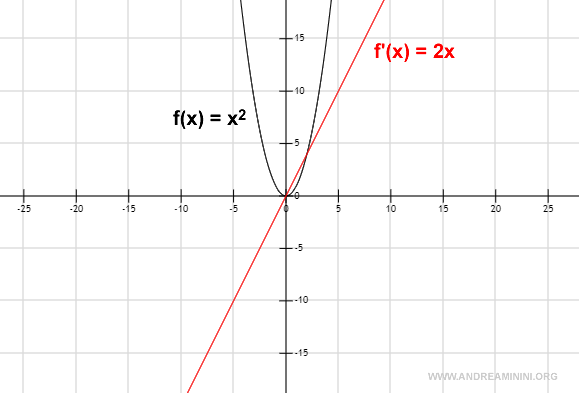
Let’s consider the following function:

$$ f(x) = x^2 $$

Using the power rule, the first derivative of f(x) is:

$$ f'(x) = 2 \cdot x^{2-1} = 2x $$

To verify this, we can compute the limit definition of the derivative:

$$ f'(x) = \lim_{h \rightarrow 0} \frac{f(x+h)-f(x)}{h} $$

Given:

$$ f(x) = x^2 $$

$$ f(x+h) = (x+h)^2 $$

Substituting into the difference quotient gives:

$$ f'(x) = \lim_{h \rightarrow 0} \frac{(x+h)^2 - x^2}{h} $$

Expanding the numerator:

$$ f'(x) = \lim_{h \rightarrow 0} \frac{x^2 + 2xh + h^2 - x^2}{h} $$

$$ f'(x) = \lim_{h \rightarrow 0} \frac{2xh + h^2}{h} $$

$$ f'(x) = \lim_{h \rightarrow 0} \bigl(2x + h\bigr) $$

As h approaches zero, we find:

$$ f'(x) = 2x $$

So, the derivative of x² is indeed 2x, as predicted by the power rule.

Graphical Representation

Let’s now test whether the rule also holds for k + 1 when k = 2:

$$ D[x^{2+1}] $$

Rewrite x³ as the product x · x²:

$$ D[x \cdot x^2] $$

Applying the product rule results in:

$$ D[x] \cdot x^2 + x \cdot D[x^2] $$

$$ 1 \cdot x^2 + x \cdot 2x $$

$$ x^2 + 2x^2 $$

$$ 3x^2 $$

Thus, the derivative of x³ is 3x², confirming the rule for n = 3.

We have therefore demonstrated by induction that the power rule holds for any positive integer exponent.

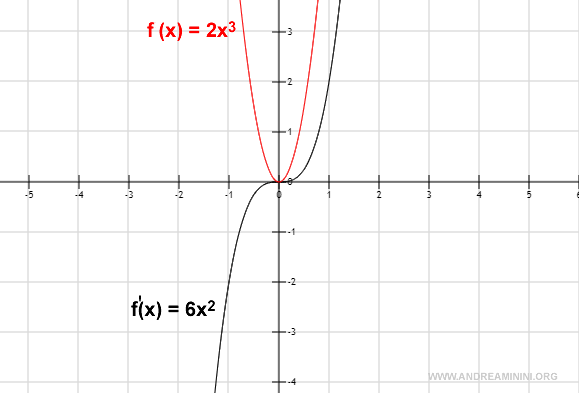
A Practical Example

Let’s compute the derivative of 2x³.

$$ f(x) = 2x^3 $$

Applying the power rule gives:

$$ f'(x) = 3 \cdot 2x^{3-1} = 6x^2 $$

Verification

We’ll verify this by evaluating the difference quotient as h approaches zero:

$$ f'(x) = \lim_{h \rightarrow 0} \frac{f(x+h)-f(x)}{h} $$

where:

$$ f(x) = 2x^3 $$

$$ f(x+h) = 2(x+h)^3 $$

Substituting into the difference quotient yields:

$$ f'(x) = \lim_{h \rightarrow 0} \frac{2(x+h)^3 - 2x^3}{h} $$

Expanding and simplifying:

$$ f'(x) = \lim_{h \rightarrow 0} \frac{2(x^3 + 3x^2h + 3xh^2 + h^3) - 2x^3}{h} $$

$$ f'(x) = \lim_{h \rightarrow 0} \frac{6x^2h + 6xh^2 + 2h^3}{h} $$

$$ f'(x) = \lim_{h \rightarrow 0} \bigl(6x^2 + 6xh + 2h^2\bigr) $$

As h approaches zero, the terms involving h vanish, leaving:

$$ f'(x) = 6x^2 $$

This confirms that the derivative of 2x³ is indeed 6x².

Graphical Representation