Derivative of a Linear Function
Definition
The derivative of a linear function f(x)=mx+n is simply the constant coefficient m. $$ f(x)=mx+n \:\: \rightarrow \:\: f'(x)=m $$
This result is straightforward to prove.
Proof
Consider a linear function f(x) defined on the interval (a, b), and any point x in its domain:
$$ f(x) = mx + n $$
To compute the first derivative f'(x), we apply the definition of the derivative as the limit of the difference quotient as h approaches zero:
$$ f'(x) = \lim_{h \rightarrow 0} \frac{f(x+h) - f(x)}{h} $$
We know that:
- f(x) = mx + n
- f(x+h) = m(x+h) + n
Substituting these expressions into the difference quotient gives:
$$ \lim_{h \rightarrow 0} \frac{m(x+h) + n - \big(mx + n\big)}{h} $$
$$ \lim_{h \rightarrow 0} \frac{mx + mh + n - mx - n}{h} $$
$$ \lim_{h \rightarrow 0} \frac{mh}{h} $$
$$ \lim_{h \rightarrow 0} m = m $$
This confirms that the derivative of a linear function is equal to its slope m.
A Practical Example
Let’s examine the following linear function:
$$ f(x) = 4x + 2 $$
The graph of this function looks like this:
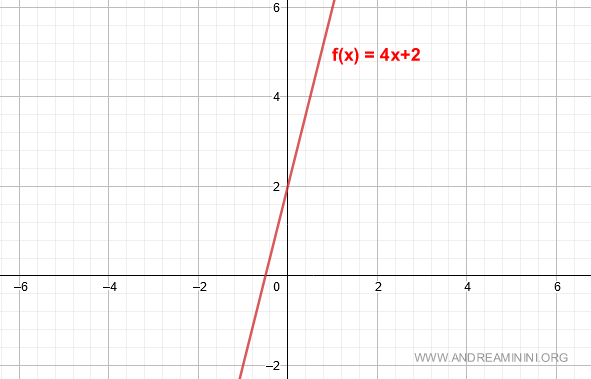
We’ll find the derivative of f(x) using the limit definition at an arbitrary point x:
$$ f'(x)= \lim_{h \rightarrow 0} \frac{f(x+h) - f(x)}{h} $$
Since:
- f(x) = 4x + 2
- f(x+h) = 4(x+h) + 2
Substituting into the difference quotient yields:
$$ f'(x)= \lim_{h \rightarrow 0} \frac{4(x+h)+2 - \big(4x+2\big)}{h} $$
$$ f'(x)= \lim_{h \rightarrow 0} \frac{4x + 4h + 2 - 4x - 2}{h} $$
$$ f'(x)= \lim_{h \rightarrow 0} \frac{4h}{h} = 4 $$
Therefore:
$$ f'(x)= 4 $$
The derivative of f(x) is the constant coefficient m of the linear function - in this case, 4.
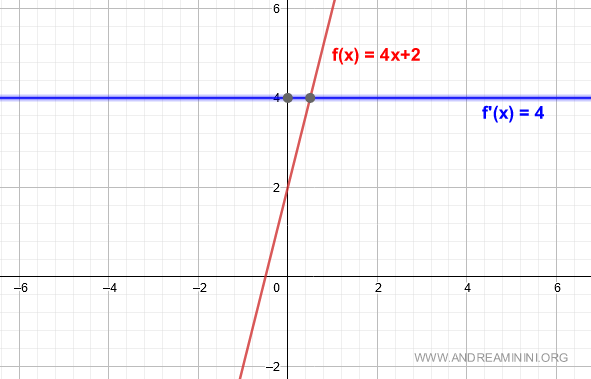
And so on.
