Geometric Interpretation of the Derivative

Geometrically speaking, the derivative of a function describes the slope of its graph at a point x₀ - that is, the gradient of the tangent line at x₀.

The equation of the tangent line to the graph at the point (x₀, f(x₀)) is:

$$ y = f(x_0) + f'(x_0) \cdot (x - x_0) $$

Proof

The function f(x) is defined in a neighborhood around x₀.

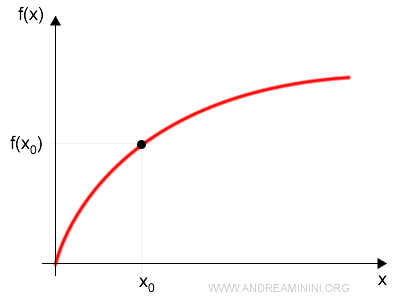
The equation of a line passing through x₀ can be written as:

$$ f(x_0) = m x_0 + q $$

Note. The variables m and q are unknowns. This equation therefore represents infinitely many lines passing through the point x₀, forming what’s known as a pencil of lines centered at that point. Among these lines is the unique tangent line at x₀.

Now, let’s consider another point x within the domain of the function.

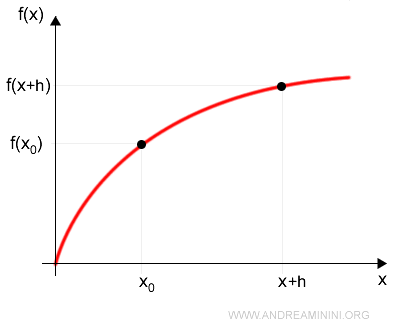
The equation of a line passing through x is:

$$ f(x_0 + h) = m (x_0 + h) + q $$

Note. Again, m and q are unknowns. Thus, this equation describes all lines passing through the point x, forming another pencil of lines centered at that point.

As a result, the secant line passing through the points x₀ and x can be determined by the following system of equations:

$$ \begin{cases} f(x_0) = m x_0 + q \\ f(x_0 + h) = m (x_0 + h) + q \end{cases} $$

The unknowns m and q can be solved from this system, first finding m and then q.

This yields the equation of the secant line through x₀ and x:

$$ y = f(x_0) + \frac{f(x_0 + h) - f(x_0)}{h} \, (x - x_0) $$

Note. The algebraic steps are as follows: $$ \begin{cases} f(x_0) = m x_0 + q \\ f(x_0 + h) = m (x_0 + h) + q \end{cases} $$ $$ \begin{cases} q = f(x_0) - m x_0 \\ f(x_0 + h) = m (x_0 + h) + \bigl(f(x_0) - m x_0\bigr) \end{cases} $$ $$ \begin{cases} q = f(x_0) - m x_0 \\ f(x_0 + h) = m x_0 + m h + f(x_0) - m x_0 \end{cases} $$ $$ \begin{cases} q = f(x_0) - m x_0 \\ \frac{f(x_0 + h) - f(x_0)}{h} = m \end{cases} $$ $$ \begin{cases} q = f(x_0) - \left(\frac{f(x_0 + h) - f(x_0)}{h}\right) x_0 \\ m = \frac{f(x_0 + h) - f(x_0)}{h} \end{cases} $$ We’ve thus determined the values of m and q for the secant line y = m x + q $$ y = m x + q $$ $$ y = \frac{f(x_0 + h) - f(x_0)}{h} \, x + f(x_0) - \left(\frac{f(x_0 + h) - f(x_0)}{h}\right) x_0 $$ $$ y = \frac{f(x_0 + h) - f(x_0)}{h} (x - x_0) + f(x_0) $$

Graphically, the secant line appears as follows:

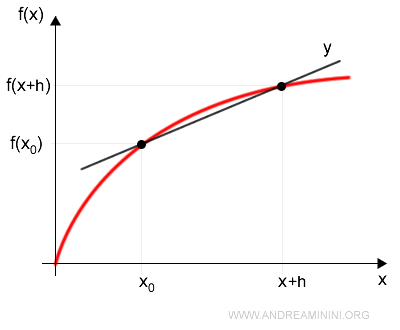
To determine the equation of the tangent line at x₀, we take the limit of the secant line as h approaches zero:

$$ y_t = \lim_{h \rightarrow 0} \left[ f(x_0) + \frac{f(x_0 + h) - f(x_0)}{h} \, (x - x_0) \right] $$

$$ y_t = f(x_0) + \lim_{h \rightarrow 0} \frac{f(x_0 + h) - f(x_0)}{h} \, (x - x_0) $$

$$ y_t = f(x_0) + f'(x_0) \cdot (x - x_0) $$

This shows that the slope of the tangent line is equal to the derivative of the function f'(x) evaluated at x₀.

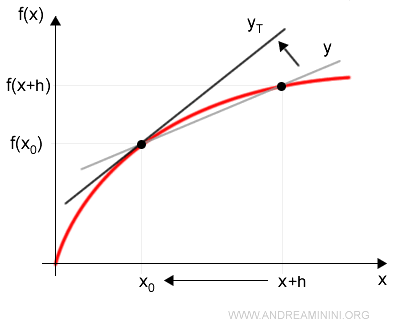
In short, the derivative of a function at x₀ determines the slope of the tangent line at that point.

And so on.