Derivative of a Constant

The derivative of any constant function is zero. $$ f(x)=k \:\: \rightarrow \:\: f'(x)=0 $$

This result is easy to prove.

Proof

Consider a function f(x) defined on the interval (a, b), and let x be any point within its domain.

$$ f(x)= k $$

For every value in the domain, the function f(x) consistently returns the same value k.

The graph of such a function appears as follows:

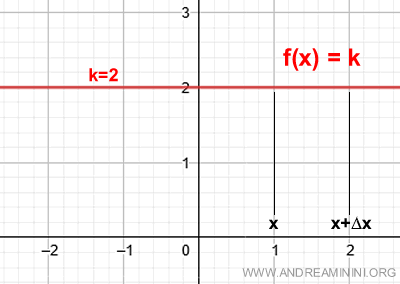
the graph of a constant function

To determine the derivative of the function, we calculate the limit of the difference quotient:

$$ \lim_{\Delta x \rightarrow 0} \frac{f(x+\Delta x)-f(x)}{\Delta x} $$

We already know that:

Therefore, we can rewrite the difference quotient as follows:

$$ \lim_{\Delta x \rightarrow 0} \frac{k - k}{\Delta x} = \lim_{\Delta x \rightarrow 0} \frac{0}{\Delta x} = 0 $$

Thus, we’ve shown that the derivative of a constant function is indeed zero.

Let’s examine the following function:

$$ f(x) = 2 $$

We calculate the limit of the difference quotient as Δx approaches zero:

$$ \lim_{\Delta x \rightarrow 0} \frac{f(x+\Delta x)-f(x)}{\Delta x} $$

Given that:

The limit simplifies to:

$$ \lim_{\Delta x \rightarrow 0} \frac{2 - 2}{\Delta x} = 0 $$

Therefore, the derivative f'(x) equals zero for every point in the function’s domain.

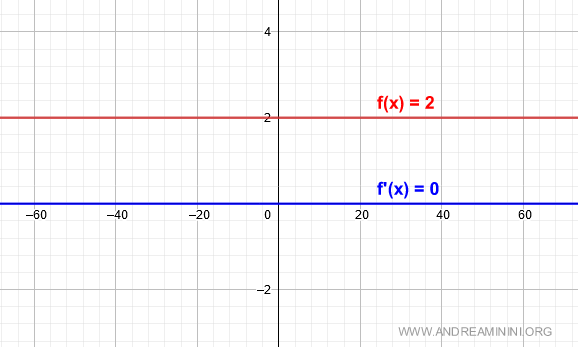
the graph of the derivative of a constant function

And so on.