Derivative of the Sine Function

The derivative of the sine function is the cosine function. $$ D[\sin x] = \cos x $$

Proof

To prove this fundamental rule of differentiation, we start with the sine function:

$$ f(x) = \sin x $$

We then consider the limit definition of the derivative:

$$ \lim_{h \rightarrow 0} \frac{f(x+h) - f(x)}{h} $$

where:

$$ f(x) = \sin x $$

$$ f(x+h) = \sin (x + h) $$

Substituting these into the difference quotient, we get:

$$ \lim_{h \rightarrow 0} \frac{\sin (x + h) - \sin (x)}{h} $$

Using the trigonometric identity: $$ \sin a - \sin b = 2 \cdot \sin \left(\frac{a - b}{2}\right) \cdot \cos \left(\frac{a + b}{2}\right) $$

we can rewrite the numerator as:

$$ \lim_{h \rightarrow 0} \frac{2 \cdot \sin \left(\frac{h}{2}\right) \cdot \cos \left(x + \frac{h}{2}\right)}{h} $$

Rewriting the expression gives:

$$ \lim_{h \rightarrow 0} \frac{\sin \left(\frac{h}{2}\right) \cdot \cos \left(x + \frac{h}{2}\right)}{\frac{h}{2}} $$

This allows us to split the limit into two parts:

$$ \lim_{h \rightarrow 0} \frac{\sin \left(\frac{h}{2}\right)}{\frac{h}{2}} \cdot \lim_{h \rightarrow 0} \cos \left(x + \frac{h}{2}\right) $$

The first limit is a standard result:

$$ \lim_{t \rightarrow 0} \frac{\sin t}{t} = 1 $$

Therefore, the expression simplifies to:

$$ 1 \cdot \lim_{h \rightarrow 0} \cos \left(x + \frac{h}{2}\right) $$

As \( h \) approaches zero, this limit evaluates to \(\cos x\):

$$ 1 \cdot \cos x $$

Thus, the derivative of \(\sin(x)\) is:

$$ f'(x) = \cos x $$

We have therefore established that the derivative of the sine function is the cosine function.

Graphical Representation

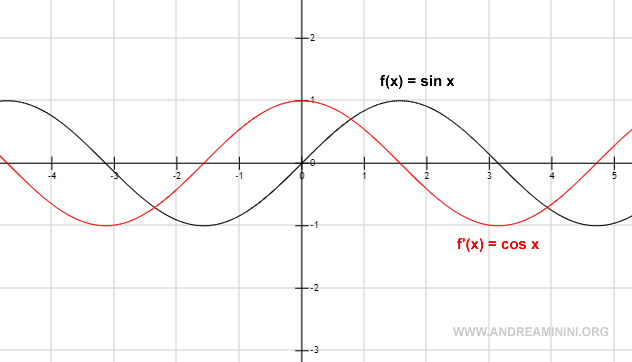
A Practical Example

Consider the following example:

$$ f(x) = \sin (x^2) $$

Note: When the argument of the sine function is something other than simply \( x \), we cannot directly apply the elementary derivative rule. Instead, we are dealing with a composite function of the form \( f(g(x)) \). Therefore, the derivative of this function is not simply \(\cos(x^2)\).

This is a classic case of a composite function, so we must apply the chain rule:

$$ f'(x) = f'(g(x)) \cdot g'(x) $$

In this case:

$$ f'(g(x)) = D[\sin(g(x))] = \cos(x^2) $$

$$ g'(x) = D[x^2] = 2x $$

Substituting these into the chain rule gives:

$$ f'(x) = \cos(x^2) \cdot 2x $$

Thus, the derivative of \(\sin(x^2)\) is:

$$ f'(x) = 2x \cdot \cos(x^2) $$

Graphical Representation

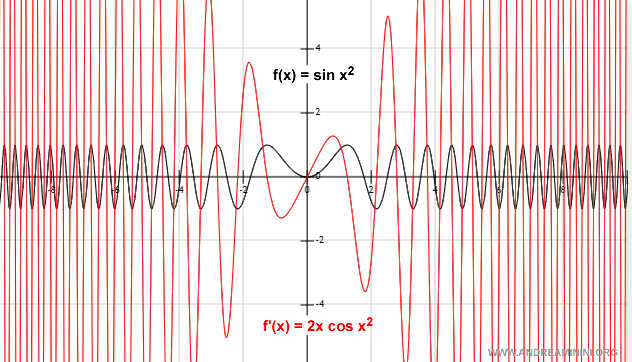
And so on.