Derivative of the Cosine Function

Definition

The derivative of the cosine function is: $$ D[\cos x] = -\sin x $$

Proof

Let’s derive this result by evaluating the difference quotient for the cosine function:

$$ \lim_{h \rightarrow 0} \frac{\cos(x+h) - \cos(x)}{h} $$

We start by using the following trigonometric identity:

$$ \cos a - \cos b = -2 \sin \left(\frac{a - b}{2}\right) \cdot \sin \left(\frac{a + b}{2}\right) $$

Applying this identity to the numerator, we set:

$$ a = x + h $$

$$ b = x $$

This transforms the difference quotient into:

$$ \lim_{h \rightarrow 0} \frac{-2 \cdot \sin \left(\frac{h}{2}\right) \cdot \sin \left(x + \frac{h}{2}\right)}{h} $$

Multiplying the numerator and denominator by \( \frac{1}{2} \) allows us to simplify the expression further:

$$ \lim_{h \rightarrow 0} \frac{-\sin \left(\frac{h}{2}\right) \cdot \sin \left(x + \frac{h}{2}\right)}{\frac{h}{2}} $$

We can separate this limit into two parts:

$$ \lim_{h \rightarrow 0} \frac{-\sin \left(\frac{h}{2}\right)}{\frac{h}{2}} \cdot \lim_{h \rightarrow 0} \sin \left(x + \frac{h}{2}\right) $$

Let’s evaluate these limits individually.

The first limit is a well-known standard limit in calculus:

$$ \lim_{t \rightarrow 0} \frac{\sin t}{t} = 1 $$

Substituting \( t = \frac{h}{2} \), we find:

$$ \lim_{h \rightarrow 0} \frac{-\sin \left(\frac{h}{2}\right)}{\frac{h}{2}} = -1 $$

The second limit is straightforward:

$$ \lim_{h \rightarrow 0} \sin \left(x + \frac{h}{2}\right) = \sin x $$

Combining these results, we get:

$$ \lim_{h \rightarrow 0} \frac{-\sin \left(\frac{h}{2}\right)}{\frac{h}{2}} \cdot \lim_{h \rightarrow 0} \sin \left(x + \frac{h}{2}\right) = -1 \cdot \sin x $$

Therefore, the derivative of \(\cos x\) is:

$$ f'(x) = -\sin x $$

We have thus proven that the derivative of the cosine function is indeed \(-\sin x\).

Graphical Representation

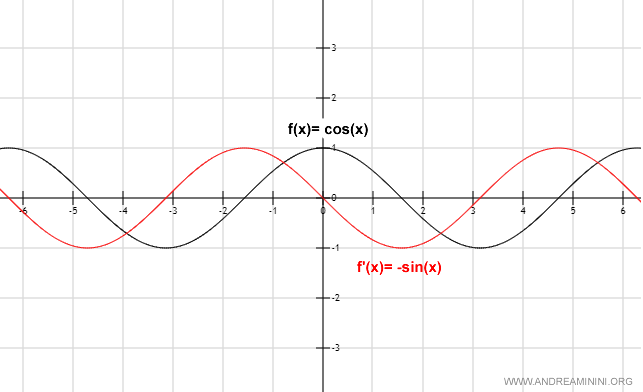
A Practical Example

Let’s examine the following function:

$$ f(x) = \cos (x^2) $$

Note: When the argument of the cosine function is not simply \( x \), we’re dealing with a composite function of the form \( f(g(x)) \). Therefore, the derivative is not simply \(-\sin(x^2)\); we need to apply the chain rule.

Since this is a composite function, we apply the chain rule:

$$ f'(x) = f'(g(x)) \cdot g'(x) $$

In this case:

$$ f'(g(x)) = D[\cos(g(x))] = -\sin(x^2) $$

$$ g'(x) = D[x^2] = 2x $$

Substituting these into the chain rule gives:

$$ f'(x) = -\sin(x^2) \cdot 2x $$

Hence, the derivative of \(\cos(x^2)\) is:

$$ f'(x) = -2x \cdot \sin(x^2) $$

Graphical Representation

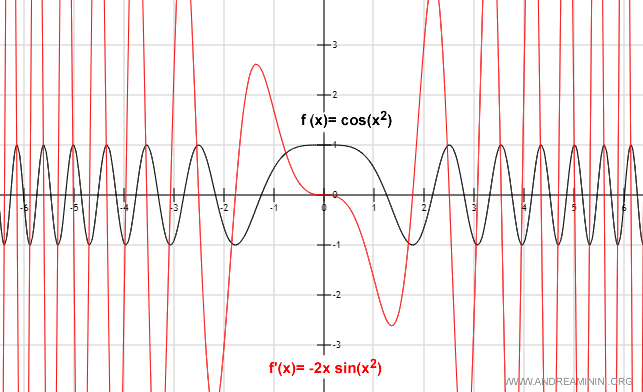
And so on.