Derivative of a Unit Vector

What is the derivative of a unit vector?

The derivative of a unit vector (u) is a vector (v) that’s always perpendicular to the unit vector itself. $$ \frac{d \vec{u}}{dt} = \vec{v} \ \ \ where \ \ \ \vec{v} \perp \vec{u} $$

For any unit vector u, its derivative is an orthogonal vector to u - that is, a vector forming a 90° angle with u.

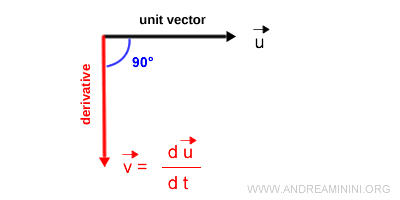
The derivative of the unit vector lies along the normal direction relative to u and can point in either direction along that normal.

Note. In the proof below, I’ll go through all the steps that show why this is true. To fully understand it, you should be familiar with the dot product of vectors.

Proof

Let’s start with an arbitrary unit vector

$$ \vec{u} $$

A unit vector is simply a vector whose magnitude equals one.

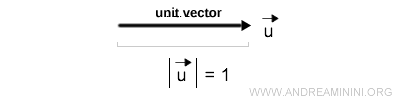
Note. A unit vector can point in any direction or orientation. For this proof, I’m choosing a direction parallel to the x-axis to make it easier to visualize the angles involved.

Let’s compute the dot product of the unit vector with itself:

$$ \vec{u} \cdot \vec{u} = |u| \cdot |u| \cdot \cos \alpha $$

Here, |u| represents the magnitude of the vector, and α is the angle between the two vectors in the dot product.

Since we’re taking the dot product of u with itself, the angle α is zero.

$$ \vec{u} \cdot \vec{u} = |u| \cdot |u| \cdot \cos 0 $$

The cosine of zero is cos(0) = 1.

$$ \vec{u} \cdot \vec{u} = |u| \cdot |u| \cdot 1 $$

$$ \vec{u} \cdot \vec{u} = |u| \cdot |u| $$

Since u is a unit vector, its magnitude is 1, so |u| = 1.

$$ \vec{u} \cdot \vec{u} = |u| \cdot |u| $$

$$ \vec{u} \cdot \vec{u} = 1 \cdot 1 $$

Thus, the dot product of a unit vector with itself equals one:

$$ \vec{u} \cdot \vec{u} = 1 $$

Next, let’s differentiate this dot product with respect to time:

$$ \frac{d (\vec{u} \cdot \vec{u}) }{dt} $$

Since the dot product equals 1, its derivative becomes the derivative of a constant, which is zero:

$$ \frac{d (\vec{u} \cdot \vec{u}) }{dt} = \frac{d (1) }{dt} = 0 $$

Alternatively, we can differentiate the dot product using the product rule for derivatives:

$$ \frac{d (\vec{u} \cdot \vec{u}) }{dt} = \frac{d \vec{u} }{dt} \cdot \vec{u} + \vec{u} \cdot \frac{d \vec{u}}{dt}
$$

Since this derivative must match the earlier result d(1)/dt = 0, we have:

$$ \frac{d \vec{u} }{dt} \cdot \vec{u} + \vec{u} \cdot \frac{d \vec{u}}{dt} = 0 $$

Because both terms are identical, we can combine them as:

$$ 2 \left( \frac{d \vec{u} }{dt} \cdot \vec{u} \right) = 0 $$

The first factor is the number 2, which is positive, while the second factor remains unknown.

Since the entire expression equals zero, the second factor must be zero as well:

$$ \frac{d \vec{u} }{dt} \cdot \vec{u} = 0 $$

This tells us the dot product between the derivative of the unit vector and the vector itself is zero.

A dot product equals zero precisely when the two vectors are orthogonal, meaning they’re at right angles to each other.

Therefore, the derivative of the unit vector du/dt is perpendicular to the vector itself.

$$ \frac{d \vec{u} }{dt} \perp \vec{u} $$

In other words, the derivative of the unit vector lies along the normal direction to u.

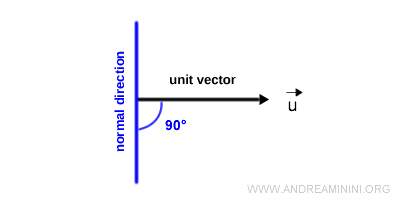
It can point either along the outer normal or the inner normal.

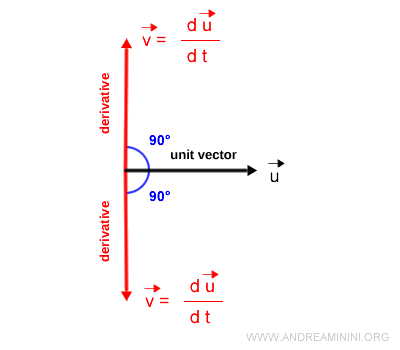
And so forth.