Right-Hand Derivative

Consider a function defined on an interval extending to the right of the point x₀. We say that f(x) is right-differentiable at x₀ if the right-hand limit of the difference quotient between x₀ and x exists and is finite as x approaches x₀ from the right. $$ f'_+(x_0) = \lim_{x \rightarrow x_0^+} \frac{f(x)-f(x_0)}{x - x_0} $$ Since Δx = x - x₀, this can also be expressed as $$ f'_+(x_0) = \lim_{Δx \rightarrow 0^+} \frac{f(x_0 + Δx) - f(x_0)}{Δx} $$ which is known as the right-hand derivative of f(x).

In this definition, we’re only concerned with the values of x lying to the right of x₀.

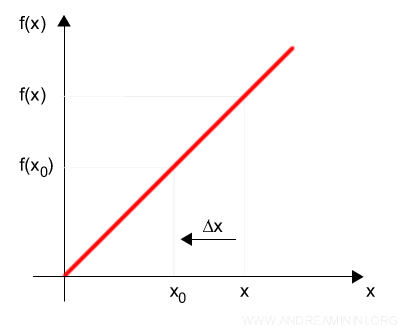
The interval to the left of x₀ isn’t taken into account.

Note. In some textbooks, the point x is written as x₀ + δ, but the idea is exactly the same. It simply refers to a point located to the right of x₀ that approaches x₀ as the limit is taken.

A Practical Example

Let’s check whether the right-hand derivative of the function f(x) = |x| exists at the point x₀ = 2.

$$ f(x) = 2 $$

We calculate the limit as x approaches x₀ from the right:

$$ f'_+(x_0) = \lim_{x \rightarrow x_0^+} \frac{f(x) - f(x_0)}{x - x_0} $$

$$ f'_+(2) = \lim_{x \rightarrow 2^+} \frac{f(x) - f(2)}{x - 2} $$

$$ f'_+(2) = \lim_{x \rightarrow 2^+} \frac{|x| - |2|}{x - 2} $$

Since x remains positive in this limit, we have:

$$ f'_+(2) = \lim_{x \rightarrow 2^+} \frac{x - 2}{x - 2} = +1 $$

So, the right-hand derivative of f(x) at x₀ = 2 is +1.

And that’s how it works.