Differential Calculus

What is Differential Calculus?

Here’s one way differential calculus is defined in mathematical analysis:

Differential calculus deals with how functions change in response to infinitesimally small variations. One of its core operations is differentiation.

That definition is quite concise - perhaps too concise - and doesn’t fully capture what’s going on, especially for someone encountering the subject for the first time.

So let’s explore it through a practical example.

A Practical Example

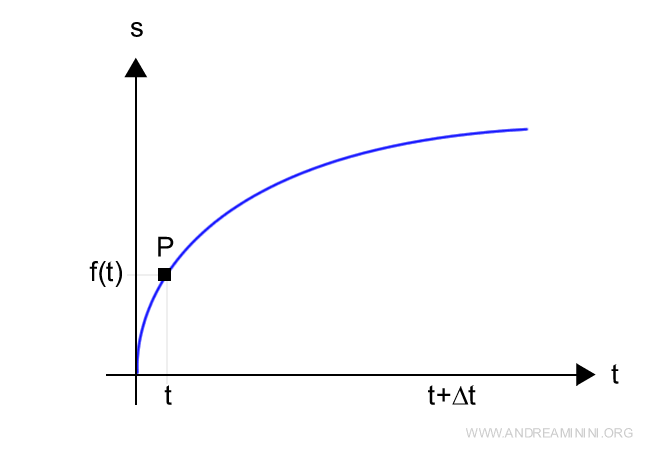
Imagine a point P moving along a path described by a function f(t).

The distance travelled by point P from an initial position is expressed as a function of time (t):

$$ s = f(t) $$

Note. Another way to describe it would be to say that the position of point P on a number line depends on time. However, that explanation tends to be a bit less intuitive.

Let’s plot this on a Cartesian plane, putting distance s on the vertical axis and time on the horizontal axis.

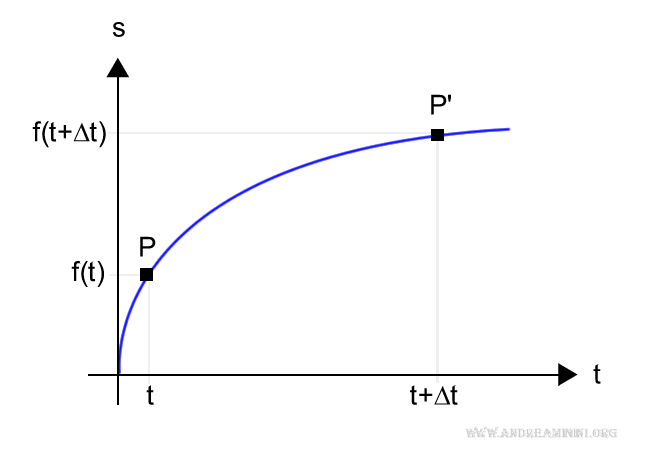
After a short interval of time Δt, the new distance travelled, s′, is given by:

$$ s' = f(t + \Delta t) $$

We then plot the new point P′ on the graph:

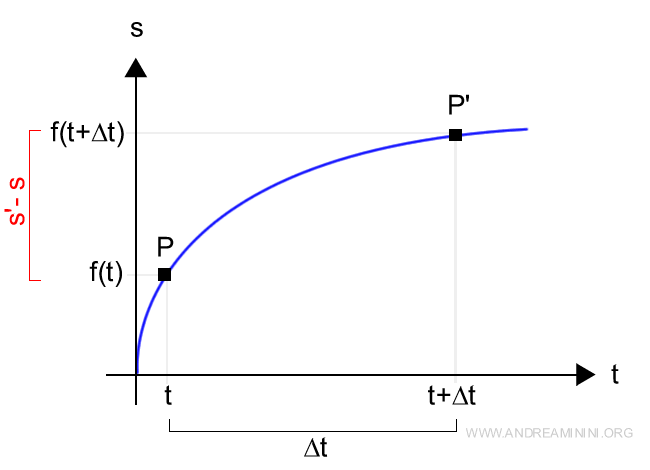
To figure out how far the point travels between the two times t and t + Δt, we calculate the difference:

$$ s' - s = f(t + \Delta t) - f(t) $$

Visually, on the graph, this looks like:

To find the average speed over this interval, we compute:

$$ \frac{f(t + \Delta t) - f(t)}{\Delta t} $$

This ratio is known as the difference quotient of the function.

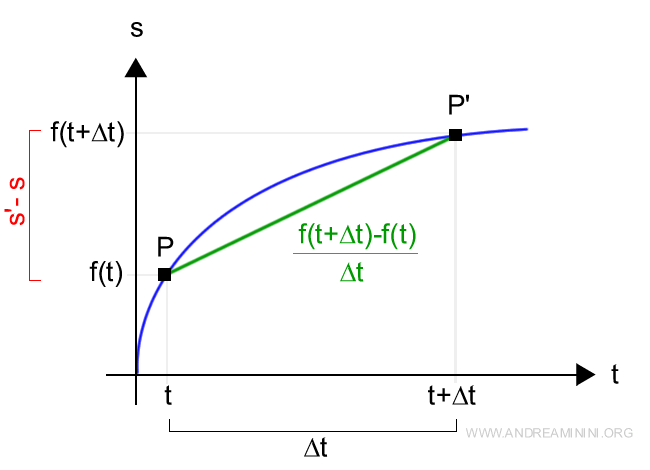
But suppose we want to know the speed of the point at an exact moment - for instance, precisely at point P. The average speed won’t tell us that, because the speed isn’t constant over time. It might start out fast, then slow down.

How do we calculate instantaneous speed?

To determine the instantaneous speed at time t - written as v(t) - we take the limit of the difference quotient as Δt approaches zero:

$$ v(t)= \lim_{\Delta t \rightarrow 0} \frac{f(t + \Delta t) - f(t)}{\Delta t} $$

This gives us a way to compute the exact speed of point P at any given instant t.

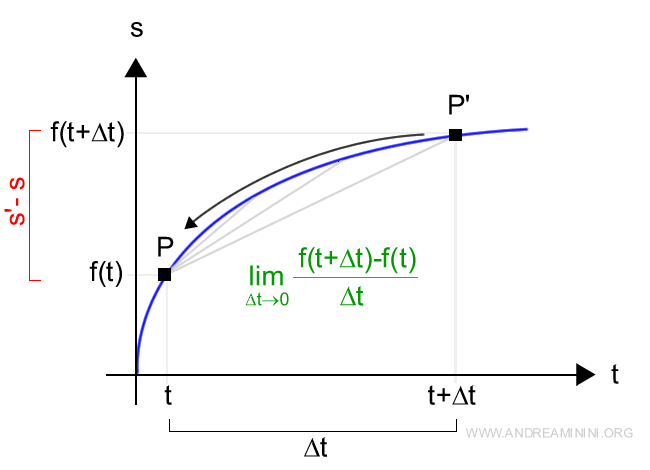
Taking the limit of the difference quotient tells us the instantaneous speed at time t.

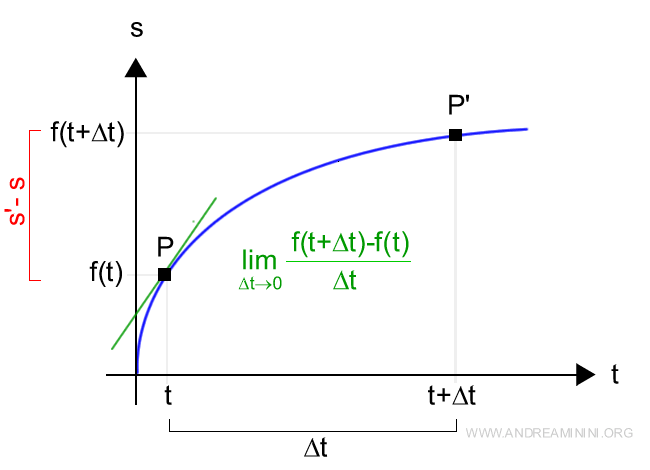
The instantaneous speed is represented by the slope of the tangent line at point P.

Taking the limit of the difference quotient is the process we call differentiation.

Why do we use differential calculus?

Differential calculus allows us to analyze how a function behaves at every single point along its curve.

It helps us determine whether the function is increasing or decreasing, whether the curve is concave or convex, whether there are asymptotes, and much more.

And so on.