Limits

What Is a Limit?

A limit is a fundamental concept in mathematics that helps us analyze how a function or a sequence behaves as its input x (for functions) or its index n (for sequences) approaches a particular value x₀, whether finite or infinite. $$ \lim_{x \rightarrow x_0 } $$

Limit of a Sequence

The limit of a sequence a_n describes how the terms of the sequence behave as the index n grows larger and larger.

$$ \lim_{n \rightarrow x_0 } a_n = l $$

Here, x₀ may be a finite real number or positive or negative infinity.

Limit of a Function

The limit of a function f(x) tells us how the function behaves as its variable x approaches a particular value x₀.

$$ \lim_{x \rightarrow x_0 } f(x) = l $$

Again, x₀ can be finite or extend to positive or negative infinity.

The General Definition of a Limit

The concept of a limit can be defined in a unified way for both sequences and functions, since a sequence is simply a special kind of function f: N → R.

Moreover, from any function f(x), we can construct a sequence by defining a_n = f(n) for all n ∈ N.

Let f(x) be a function defined on a set I ⊆ R, and let x₀ ∈ (-∞, +∞) be an accumulation point of I. We say that f(x) has a limit equal to l ∈ (-∞, +∞) as x approaches x₀ if, for every neighborhood U of l, there exists a neighborhood V of x₀ such that $$ x \in V \setminus \{x_0\} \Rightarrow f(x) \in U $$

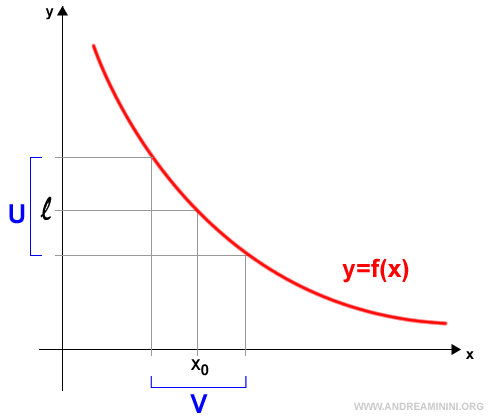
Since the set of natural numbers N has only one accumulation point at positive infinity, when dealing with sequences we consider the limit solely as n → ∞.

$$ \lim_{n \rightarrow \infty} a_n = l $$

Below is a graphical illustration of the limit of a sequence a_n.

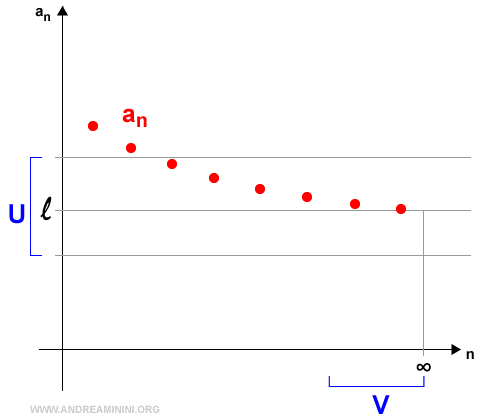
And so on.